In a Spin
Problem
What is the volume of the solid formed by rotating this right angled triangle about the hypotenuse?
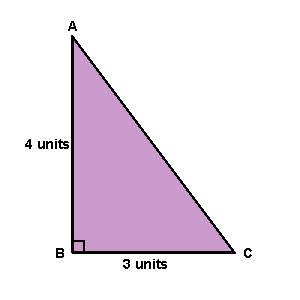
Can you generalise this for any right angled triangle with sides of length $a$, $b$ and $c$, where $b$ is the hypotenuse?
Student Solutions
Correct solutions were received from Joshua T. and Andrew I. Congratulations to both of you. I have used a mixture of the solutions to form the basis of what follows.
The first thing to observe is that by rotating the triangle about the hypotenuse I obtain two cones having the same base and opposite vertices.
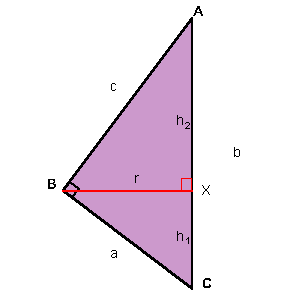
To find the volume of a cone you need its height and the radius of its base. So you need to calculate the radius and the height of each cone.
$$V = \frac{1}{3}\pi r^2 h$$
The radius of the base of the cones is the altitude of the right-angled triangle ($r$), and the corresponding heights are $AX$ and $CX$.
Working directly on the general case - as it seems simpler. Let the sides of the triangle be $a$, $c$ and $b$ ($b$- the hypotenuse).
\begin{eqnarray}V &=& \frac{1}{3}\pi r^2 h \\ &=& \frac{1}{3}\pi r^2 h_{1}+\frac{1}{3}\pi r^2 h_{2}\\ &=&\frac{1}{3}\pi r^2 (h_{1}+h_{2}) \\ &=& \frac{1}{3}\pi r^2 b \end{eqnarray}
Finding the area of a right-angled triangle in two ways:
$$\frac{ac}{2}=\frac{rb}{2}$$
Therefore $$r = \frac{ac}{b}$$
Substituting for $r$ in the equation for the volume you get:
\begin{eqnarray} V &=& \frac{1}{3}\pi r^2 b \\ &=& \frac{1}{3}\pi \left( {\frac{{ac}}{b}} \right)^2 b \\ &=& \frac{1}{3}\pi \frac{{(ac)}^2}{b}\end{eqnarray}
From here you can substitute for the particular case given at the start of the problem.
