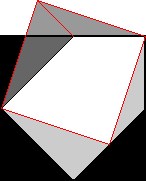
Take a Square
Cut off three right angled isosceles triangles to produce a
pentagon. With two lines, cut the pentagon into three parts which
can be rearranged into another square.
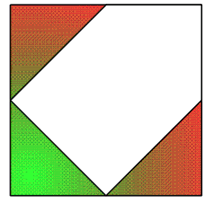
Problem
Cut off three congruent right angled isosceles triangles to produce a pentagon.
With two lines, cut the pentagon into three parts which can be rearranged into another square.
Image
Getting Started
What is the area of the pentagon?
This tells you the area of the square and so the length of its sides.
Student Solutions
Correct solutions were received from Thomas and from Isabelle of Lathallan School. Well done to both! Here is Isabelle's solution, with diagrams added by the editor.
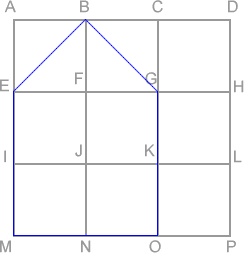
I redrew the pentagon inside a $3 \times 3$ grid of $9$ small squares (all the same size). The across lines were $ABCD$; $EFGH$; $IJKL$; $MNOP$. The down lines were $AEIM$; $BFJN$; $CGKO$; $DHLP$. The pentagon was $BGOMEB$. (This is shown on the diagram below, with the pentagon drawn in blue. Can you see why this is the same as the original pentagon? --Ed.)
Image
As lines $EB$ and $BG$ cut their small squares into halves, the triangle $EBG$ has the same area as each of the nine small squares. The rest of the pentagon is $4$ small squares so all of it is the same as $5$ small squares. The whole area is $9$ small squares so I need to find a square inside, which is just $4$ small squares smaller. Then I noticed that if I drew line $IO$, it would cut the rectangle $IKOM$ in half, making triangle $IMO$ the same as $1$ small square. Then I saw that I could draw $BIOH$ as a square which is surrounded by $4$ triangles each $1$ small square in size. (This is shown in red on the second diagram -- Ed.)
Image
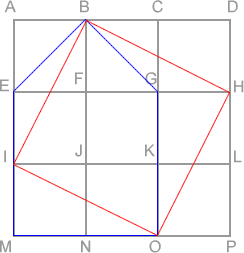
So this new square is $9 - 4 = 5$ small squares in size. Now I could see that if I cut out $EBI$ from the original pentagon, it would fit into $BGH$, and $IMO$ would fit into $OGH$. This means that I could turn the pentagon into a square by cutting along $BI$ and along $IO$ and simply rearranging the pieces.
A slightly different approach was taken by Thomas, whose solution is given below. Can you see the similarities and differences between the two ways of solving the problem? (Again, the editor has added diagrams.)
From the midpoint of the left side of the square, draw a line to the midpoint of the diagonal connecting the bottom and right sides ($BF$). From this point, draw the second line to the upper right corner of the square ($FE$).
Image
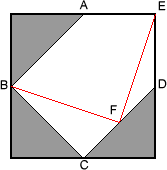
Why? $3/8$ of the square is lost when the triangles are cut away, so, assuming a unit square, the area of the pentagon (and subsequent square) is $5/8$; this requires a new square with sides of length $\frac{\sqrt{10}}{4}$.
The first line makes a triangle ($BCF$) that, once flipped over and placed with $BC$ along edge $AB$, makes a right angle and two sides of the desired length. We can check that $BF$ is of the right length using Pythagoras' theorem.
Triangle $DEF$, formed by the second line, has a longest side also of the desired length. We know the lengths of $DE$ and $DF$ ($\frac{1}{2}$ and $\frac{\sqrt{2}}{4}$) and the angle $EDF$ between them ($135$ degrees) and so can use the law of cosines $(c^2 = a^2 + b^2 - 2 a b \cos C)$. This gives $$EF^2 =\left(\frac{1}{2}\right)^2 + \left(\frac{\sqrt{2}}{4}\right)^2 - 2 \frac{1}{2} \frac{\sqrt{2}}{4} \frac{-\sqrt{2}}{2} =\frac{5}{8}; $$ thus $$EF = \sqrt{\frac{5}{8}} = \frac{\sqrt{10}}{4}$$ Thus if we move the second triangle so that $DE$ lies along $AD$, we see that we have formed a square of side $\frac{\sqrt{10}}{4}$.
The rearrangement is shown below.
Image