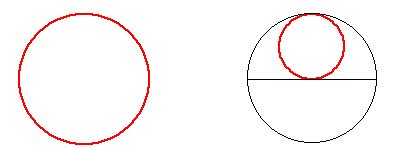
Semi-square
Problem
What is the ratio of the area of a square inscribed in a semicircle to the area of the square inscribed in the entire circle?
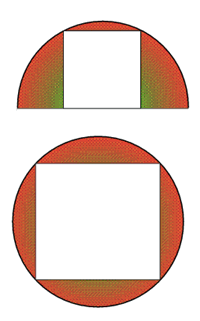
Getting Started
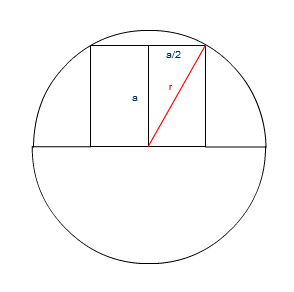
Let the radius of the circle be r, and the side length of the square in the semicircle be a. Can you work out a in terms of r?
Student Solutions
A well presented solution from Deepak of Queen Mary's College Walsall is given below. Correct solutions were also recieved from Andrei of School 205 Bucharest and Calum of Madras College.
Other students from Madras College extended the problem to look at other polygons inscribed inside a circle and a semi-circle. Some of their work follows the solution to the initial problem. This should make you think about what many NRICH problems have lying beneath the skin!! They think they have discovered a pattern - what do you think? My very very many thanks to Thomas Sheila and Elaine and their teacher Ken Nisbet for sending me their work. Keep it up (all I need now is the electronic version!!).
In the beginning there was:
In the first diagram the radius of the circle is $r$ and the side of the square is $2y$ units
Area of the square is
$$ (2y)^2 = 4y^2$$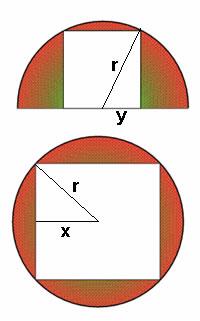
By Pythagoras, $$ y^2 + (2y)^2 = r^2$$
i.e. $$ r^2 = 5y^2$$
Thus the area of the square is
$$ \frac{4r^2}{5}$$In the second diagram the radius of the circle is $r$ and the side of the square is $2x$ units.
Area of the square is
$$ (2x)^2 = 4x^2$$By Pythagoras, $$ x^2 + x^2 = r^2$$
i.e. $$ r^2 = 2x^2$$
Hence Area of the square is
$$ 2r^2$$So the ratio of the areas is :
$$ \frac{4r^2}{5} : 2r^2 $$That is $$4/5 : 2 = 2 : 5$$
Then there was:
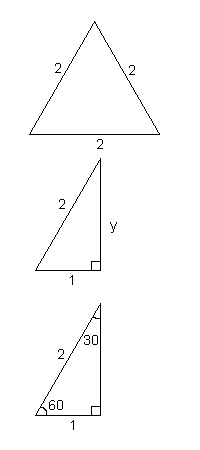
Equilateral triangles by Thomas:
Why can I state cos $30$ and sin $30$ to the exact answer?
If I split an equilateral triangle of side $2$ I will have a right-angled triangle of hypotenuse $2$ and base $1$ unit.
The angles are $30$ degrees, $60$ degrees and $90$ degrees
By Pythagoras Theorem:
\begin{eqnarray} 2^2 - 1^2&=& y^2\\ 4-1&=& y^2\\ y^2 &=& 3\\ y&=& \sqrt{3} \end{eqnarray}So
\begin{eqnarray} \mbox{sin}\; 30&=& \frac{1}{2}\\ \mbox{cos} \; 30&=& \frac {\sqrt{3}}{2}\\ \end{eqnarray}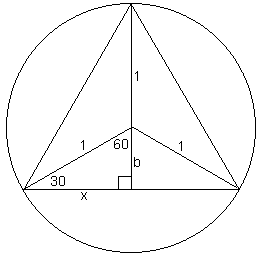
I am able to make the diameter $2$ units as all cirlces are
similar.
$x =$ half the base of the equilateral triangle
$b =$ height $- 1$ (the radius)
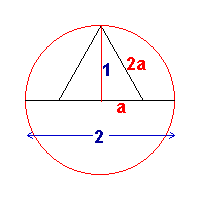
By Pythagoras Theorem
\begin{eqnarray} (2a)^2 - a^2&=& 1^2\\ 3a^2 &=& 1^2\\ a &=& \frac{1}{\sqrt{3}} \\ \end{eqnarray}Area of triangle is
$$ 2 \times\frac{1}{2} \times 1 \times \frac{1}{\sqrt{3}} = \frac{1}{\sqrt{3}}$$ sq unitsThe ratio of the areas:
$$ \frac{1}{\sqrt{3}} : \frac{3\sqrt{3}}{4} = 4:9 $$The ratio is $4:9$
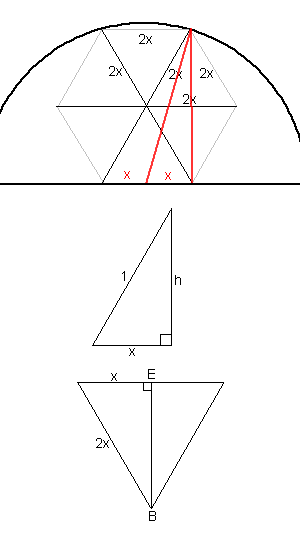
Hexagons and more by Sheila and Elaine
Area of smaller hexagon (in the semicircle)
Suppose the diameter of the circle is $2$ (all circles are similar).
The hexagon can be split into $6$ equilateral triangles.
Therefore the area of the hexagon $= 6 \times$ area of one triangle.
To find the area of the triangles we need to find $x$.
Taking the red triangle from the diagram, we know that its hypotenuse is the radius of the circle ($1$ unit) and that h is twice the height of an equilateral traingle.
Using the lower triangle
\begin{eqnarray} h&=&2 \times BE \\ BE^2&=& (2x)^2 - x^2\\ BE^2 &=&3x^2\\ EB &=& \sqrt{3} \times x \\ h &=& 2 \times \sqrt{3} \times x \\ h &=& 2 \sqrt{3} x \\ \end{eqnarray}Now we can find $x$:
\begin{eqnarray} 1^2&=& x^2 + (2 \sqrt{3} x)^2 \\ 1^2&=& x^2 + 4 \times 3 \times x^2 \\ 1^2 &=& x^2 + 12x^2\\ x &=& \frac{1}{\sqrt{13}} \end{eqnarray}Total area of hexagon $= 6 \times$area of an equilateral triangle
Area $= 6 \times \frac{1}{2} \times 2x \times \frac{h}{2} $
Area $= 3 \times x \times h $
Area $= 3 \times \frac {2}{\sqrt{13}} \times \frac{\sqrt{3}}{\sqrt{13}} $
Area $=\frac {6 \sqrt{3}}{13}$ sq units
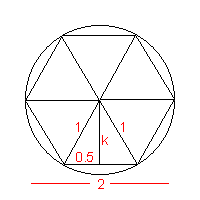
Area of larger hexagon:
The diameter of the circle is still $2$ units.
Area of hexagon $= 6 \times$area of an equilateral triangle
\begin{eqnarray} k^2&=& 1^2 - 0.5^2 \\ k^2&=& \frac{3}{4} \\ k &=& \frac{\sqrt{3}}{2}\\ \mbox{Total area} &=& 6 \times 1 \times \frac{\sqrt{3}}{2} \times \frac{1}{2} &=& \frac {3 \sqrt{3}}{2} \mbox{sq units} \end{eqnarray}So the ratio of the areas is :
$$ \frac{6 \sqrt{3}}{13} : \frac {3 \sqrt{3}}{2} $$That is $4 : 13$
Ratio of shapes
| Shapes | Triangle | Square | Pentagon | Hexagon | ....... |
|---|---|---|---|---|---|
| Smaller shape ($s$) | 4 | 4 | 4 | 4 | ....... |
| Larger shape ($b$) | 9 | 10 | ? | 13 | ....... |
| Relationship | $b=2 \frac{1}{4}s$ | $b=2\frac{2}{4}s$ | ? | $b=3\frac{3}{4}s$ | ....... |
A possible solution to the mystery pattern:
We think the value for the pentagon may be $2 \frac{3}{4}$ .
Using the Fibonacci sequence on the numerator (top number) of the fractions in the realtionship between $b$ and $s$ would give a ratio between the two areas of the pentagon as $4:11$.
If this is the case we can use this to predict the ratio of the areas of the heptagon and the octagon:
Heptagon $4:16$
Octagon $4:21$
We couldn't prove this as we didn't have enough time.
Note from the editor:
What do other members think? I have just a thought to add to this in the form of a diagram...