Square Pizza
Problem
Can you show that you can share a square pizza equally between two people by cutting it four times using vertical, horizontal and diagonal (45 degree cuts) through any point inside the square?
Based on a problem given at the 2002 ATM conference.
Getting Started
You probably need to consider the two people having alternate segments of the pizza.
You could consider the areas of all the right angled isosceles triangles.
Alternatively, you could reduce the problem considerably by removing a symmetrial portion of the pizza.
Student Solutions
Two solutions offered by Andrei of School 205, Bucharest. Many thanks Andrei.
I solved the problem in two ways:
Method 1.
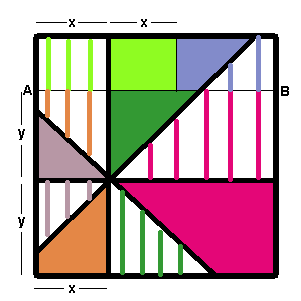
I find from reasons of symmetry the equality of areas
Without loss of generality, I suppose x < l/2, and y < l/2.
I start from the observation that there are from the beginning two congruent triangles, the one coloured in purple, and the other with purple lines.
I look now to the trapezium coloured continuously in red, and I try to find another one, congruent with this one. For this, I trace a line AB parallel to the base of the square, at 2y. It is drawn in the figure.
I see the equality of the areas of the two trapeziums the one in continuous red, the other with red lines.
The line drawn determines another 4 trapeziums, with equal areas two by two, and that could be identified from the colour: green and orange.
Now, I remained with all the area above the line AB just drawn. To find equal areas, I drew another line, parallel with the vertical side of the square, at 2x.
The equal areas found are again with the same colour, line and continuous.
Now, the part of the pizza with lines has the same area with the part of the pizza with continuous colours, and it is easy to join the parts that have been determined by the new lines.
Method 2.
I calculated the areas of all figures (triangles and rectangular trapeziums) delimitated by the sides of the pizza and by the cuts.
I noted all the points from the figure (see chart). Now, let the length of DI be x and the length of DK be y; let the side of the square be 1 unit.
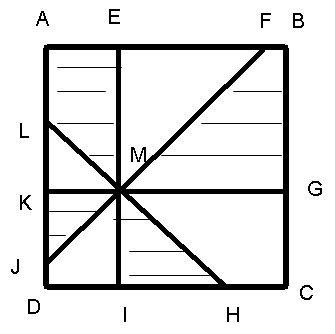
A LMK = x 2 /2
A KJM = x 2 /2
A DJMI = xy - x 2 /2
A HCGM = 1y - xy - y 2 /2
A MFBG = (1 2 - y 2 )/2 - 1x +
xy
A LAEM = 1x - xy - x 2 /2
A EMF = 1 2 /2 - 1y + y 2 /2
Now, look what areas to add to obtain 1 2 /2.
First I take triangle EMF, whose area begins with 1 2 /2. Because 1y is subtracted from 1 2 /2, I must look for an area that contains (+ 1y). The only area containing such a number is MHCG. I write the obtained area up to now:
AEMF + AHCGM = 1 2 /2 - 1y + y 2 /2 + 1y - xy - y 2 /2 = 1 2 /2 - xy
Now, I must add something containing (+xy). I add LKM and DJMI, obtaining 1 2 /2. For the remaining areas the sum is naturally 1 2 /2.
So, I added the areas in the following manner:
ALKM + ADJMI + AMHCG + AEMF and
AKJM + AMIH + AMFBG + ALAEM.
These two kind of pieces are marked differently on the figure.
