Sweets in a box
How many different shaped boxes can you design for 36 sweets in one layer? Can you arrange the sweets so that no sweets of the same colour are next to each other in any direction?
Problem
Sweets in a Box printable sheet
A sweet manufacturer has decided to design some gift boxes for a new kind of sweet.
Each box is to contain 36 sweets placed in lines in a single layer in a geometric shape without gaps or fillers.
How many different shaped boxes can you design?
The sweets come in 4 colours, 9 of each colour.
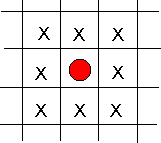
Arrange the sweets so that no sweets of the same colour are adjacent to (that is 'next to') each other in any direction. In the picture below, none of the squares marked x can have a red sweet in them.
Arrange the sweets in some of the boxes you have drawn.
Now try making boxes of 36 sweets in 2, 3 or 4 layers.
Can you arrange the sweets, 9 each of 4 colours, so that none of the same colour are on top of each other as well as not adjacent to each other in any direction?
See if you can invent a good way of showing your arrangement.
Try different numbers of sweets such as 24 or 60 in each box.
Getting Started
How many different rectangular-shaped boxes can you make using $36$ squares?
Could you make boxes in any other shape?
Student Solutions
Gabe and Zoran from Mrs. Hovish's Math Class from the Athena Academy in the United States
At first we were confused so we started by placing beads in random places. Then we started moving the "candies" around so that they would follow the rules. Then we started seeing a pattern! We noticed that the same 2 colors were always in a row together so we just finished by following that. I ended up with 6 rows and 6 columns. Gabe had 4 rows and 9 columns. We used a multiplication chart and saw that 6X6 = 36 and 9X4= 36 too! Here are their pictures.
Tamara, Ellie and Izzy, Lily and Isabelle from St. Andrew's, Enfield sent in these three solutions.
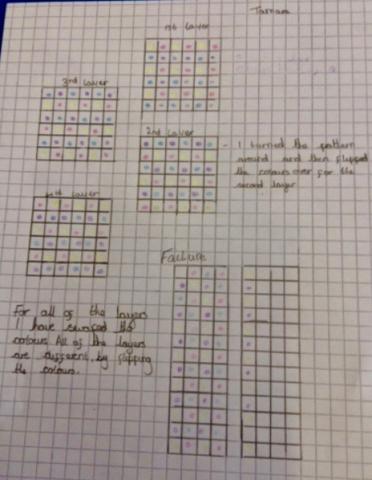
Shriya from the International School in Frankfurt Germany sent in these three excellent different designs.
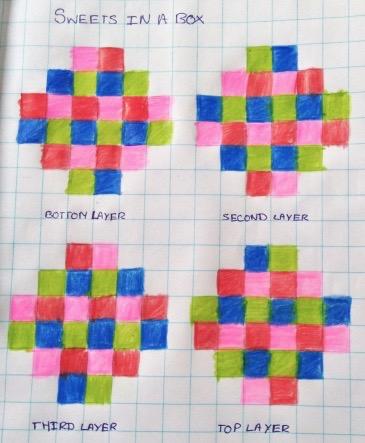
Lily and Isabelle from St.Michaels School sent in this solution:
Well these were really good solutions, well done everyone.
Teachers' Resources
Sweets in a Box
A sweet manufacturer has decided to design some gift boxes for a new kind of sweet.
Each box is to contain $36$ sweets placed in lines in a single layer in a geometric shape without gaps or fillers.
How many different shaped boxes can you design?
The sweets come in $4$ colours, $9$ of each colour.
Arrange the sweets so that no sweets of the same colour are adjacent to (that is 'next to') each other in any direction. In the diagram below none of the squares marked x can have a red sweet in them.
Arrange the sweets in some of the boxes you have drawn.
Now try making boxes of $36$ sweets in $2$, $3$ or $4$ layers.
Can you arrange the sweets, $9$ each of $4$ colours, so that none of the same colour are on top of each other as well as not adjacent to each other in any direction?
See if you can invent a good way of showing your arrangement.
Try different numbers of sweets such as $24$ or $60$ in each box.
Why do this problem?
This investigation provides pupils with an engaging context in which to explore the factors of $36$ through rectangular boxes. It will also give them a chance to pursue their own questions and take ownership of the investigation themselves.
Possible approach
Key questions
How could you arrange $36$ sweets in a rectangular box?
Are there any other ways?
What can you say about the number $36$? What are its factors?
How does that help?
How do you know you have got all the rectangular designs?
How are you going to colour your arrangement so that no sweets of the same colour are adjacent to each other?
Possible extension
Possible support
Using counters in four colours to represent the sweets will help children to try out their ideas in a less intimidating way than committing something to paper. You could use the interactivity in the Growing Garlic problem instead of counters by reducing the number to $36$.