Lens Angle
Problem
Find the missing angle in the diagram. $O$ is the centre of the circle.
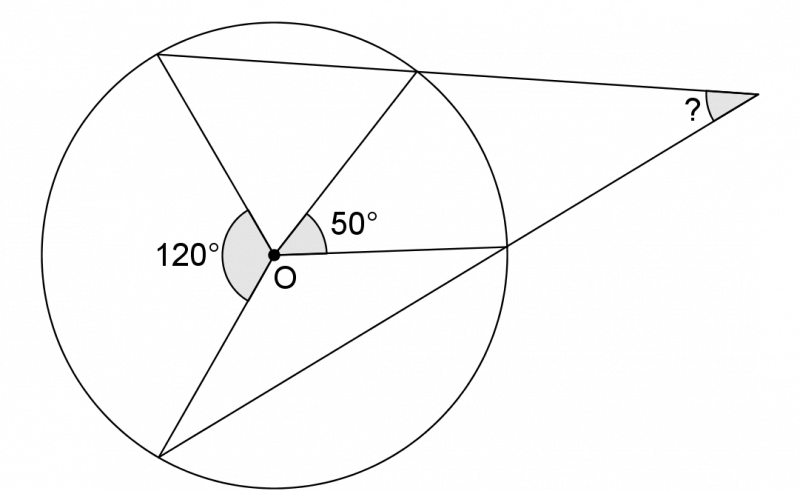
Getting Started
Isosceles triangles.
Student Solutions
There were almost as many solutions to this problem as solutions sent in! I have included four versions below. It is good to see that there is more than one way to answer most NRICH problems. Well done to all of you.
Just one general comment - some of you assumed that AOC was a diameter and, although this led to the same answer, the solution you gave was therefore not correct.
The first solution is from Julia Collins from Langley Park School for Girls, Bromley.
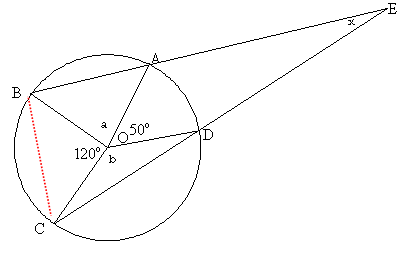
Since OC = OD, OCD is an isosceles triangle and angle OCD = angle ODC.
Angle OCD = $\frac{180 - b}{2} = 90 - \frac{b}{2}$
Similarly with triangles OCB (giving angles of $30$ ° for OBC and OCB) and OBA (giving angle OBA = $90 - \frac{a}{2}$).
Triangle BCE must have its angles adding up to 180 °.
Therefore:
$(90 - \frac{a}{2}) + 30 + 30 + (90 - \frac{b}{2}) + x = 180$
$60 + x - \frac{a}{2} - \frac{b}{2} = 0$
$120 + 2x= a + b$
The angles around the centre of the circle must add up to $360^\circ$, so $a + b = 360 - 120 - 50 = 190^\circ$
So $120 + 2x = 190$
$2x = 70$
$x = 35^\circ$
The second solution is from Andrei Lazanu from School 205, Bucharest, Romania
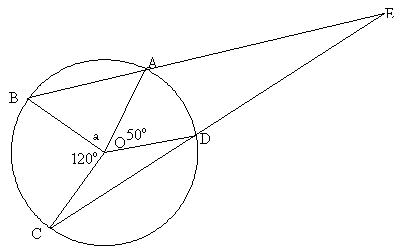
Triangles OAB and OCD are both isosceles, OA, OB, OC and OD being radii in the circle of centre O.
If a is the measure of angle AOB, the measure of angles OAB and OBA is: $${{{180^o}-a} \over 2} = 90^o - {a \over 2}$$ The measure of angle OAE is consequently: $${{180^o} - ({90^o} - {a \over 2})} = 90^o + {a \over 2}$$ Because the measure of an angle round a point is $360$ °, the measure of angle COD is: $${360^o}- ({120^o} + {50^o} + a) = {190^o} -a$$ The base angles of the isosceles triangle BOD have the measure: $${{{180^o} - ({190^o} - a)} \over 2} = {{a \over2} - {5^o}}$$ The angle ODE has the measure: $${{180^o} - ({a \over 2} - {5^o})} = {{185^o} - {a \over 2}}$$ I use now the sum of angles in the quadrilateral OAED, that is $360$ °, in order to determine the measure of angle DEA: $${360^o}- ( {50^o} + {185^o} - {a \over 2} + {90^o} + {a \over 2}) = {35^o}$$ Consequently, the measure of angle DEA is $35$ °.
Guy David from Ransom Everglades Middle, Miami, Fl, USA sent this solution
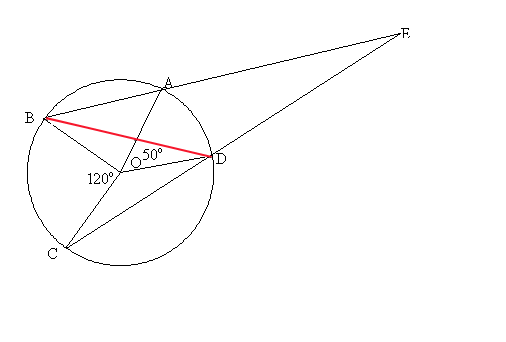
The measure of the mystery angle is $35$ degrees.
The inscribed angle in a circle is half the measure of the arc it intercepts.
First, I make chord BD. This creates an inscribed angle of measure $120^\circ /2 = 60^\circ$ at D. Which means that angle BDE is $120$o .
The chord also create an inscribed angle at B, of measure $50^\circ /2 = 25^\circ $.
We now have two angles of triangle EBD, that sum to $145$o . Therefore, the mystery angle is $180^\circ -145^\circ = 35^\circ$.
Anna Robinson, Caroline Swanson and Chloe Pickup from The City of London School for Girls
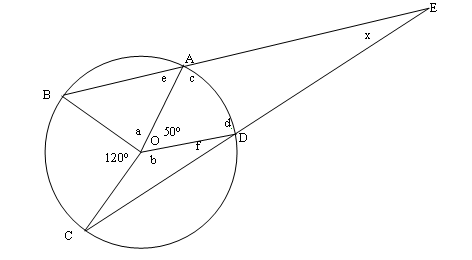
$170 + a + b =360$
$a + b = 360 - 170$
$a + b = 190$
In triangles OBA and OBC
$a + b + 2e + 2f = 360$
Therefore $2e + 2f = 360- 190$
$2e + 2f =170$ (divide by $2$)
$e + f =85$ (*)
In OAED
$50 + c + d + x = 360$
$c + d + x = 310$ (**)
$e + d + f + c = 360$ (angles on straight lines)
$c + d = 275$ (from *)
$310 - 275 = 35$ from (** and above)
Therefore $x = 35$
Teachers' Resources
Why do this problem :
This superficially fixed problem is an excellent way to draw students into the discovery of a general result. There are likely to be a range of possible routes to solution giving ample opportunity for discussion of other people's approaches and the elegance and efficiency of approaches.Possible approach :
It seems at first as though there's not enough information to fix the angle whose size we are asked to establish - parts of the construction seem to have a lot of freedom to wander.
But as this situation is explored more it becomes apparent that the angle of interest maintains its size wherever the unconstrained parts of the diagram happen to rest.
This freedom to wander may be clear to the group almost immediately but if it is not, ask the students to reproduce the figure using the given values. This should help them appreciate what hasn't been specified, and lead them to question whether it is necessary for these to be specified.
Now they have something to explore.
Dynamic Geometry may help with enquiry, but isn't essential. Two drawings of the figure with measurements of the angle should be enough to suggest a possible general result which can then be reasoned over.
In conjunction with the problem presented the following connected result can be included : allow one fixed length chord to move around a given circle, relative to a second chord of some other fixed length. Joining the end of each chord to the opposite end of the other will produce two diagonal lines which, it turns out, intersect at the same angle regardless of the relative position of the chords.
Key questions :
- Can anyone see how we could know the size of the missing angle - or any ideas how we might try to find it ?
- Any thoughts at all about the problem ?
- Can you describe how to draw this diagram ? What do you do first ? Then what ?
