Designing table mats
Problem

The photo on the right shows a table mat made from a coiled rope.
Chris wants to produce and sell sets of table mats like this. Her initial plan is to make them by coiling a thin rope into a rectangular pattern, sewing each layer to the next with 'thread' made of a strand of the material the rope is made from. Measuring a mat she already has, she decides that 30cm x 24 cm is a good size to aim for.
- Is this size possible using this method - coiling a length of rope as in this image?
- How might she rethink the design so she can make a bigger range of lengths and widths of mat?
You will need to make sensible assumptions about the thickness of the rope, and the construction of the mat including the length of the starting section of rope in the centre of the mat. Write down all the assumptions you make so you can revisit them and decide if they are acceptable.
Getting Started
Student Solutions
I'm going to start by making some basic assumptions:
- The image looks as if it might be life-size, and measuring it I find that the diameter of one rope coil is about 0.5cm, so I'm going to use that as my rope diameter.
- Again measuring from the image, the first part of the rope coil, in the centre of the mat appears to be about 1cm, so I'm going to assume a length of 1cm on the inside of the rope section and 1.5cm on the outside.
- If this is taken as the first horizontal section of rope, then the first vertical section appears to be negligible on the inside of the coil, and two rope diameters on the outside, so 1cm.
- I'm going to assume that all rope sections fit together neatly without any gaps.
- I'm going to also assume that all turns are at 90 degrees.
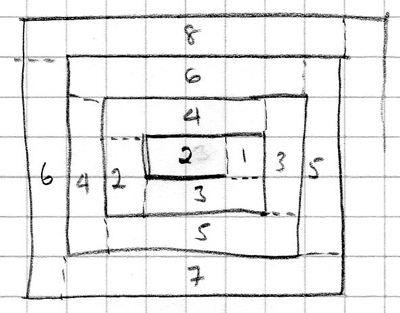
The squares are 0.5cm x 0.5cm.
The diagram shows me immediately that starting the rope coil like this means that the mat will be longer in one dimension than the other, but is 30cm x 24cm possible?
At this stage, I added dotted lines to my diagram so I could distinguish between horizontal and vertical sections (this could be done in different ways, but provided you do it consistently, exactly how you do it won't matter), and put the number of squares in each section on my diagram.
There appear to be two sequences, one for horizontal sections and one for vertical sections - yours may be different if you have divided your sections up in a different way. Tabulating (in numbers of 0.5cm squares):
| Horizontal strip length | Horizontal length (cm) | Vertical strip length (squares) | Vertical length (cm) | Total length of rope so far (cm) |
|---|---|---|---|---|
| 2 | 1 | 1 | 0.5 | 1.5 |
| 3 | 1.5 | 2 | 1 | 4 |
| 4 | 2 | 3 | 1.5 | 7.5 |
| 5 | 2.5 | 4 | 2 | 12 |
| 6 | 3 | 5 | 2.5 | 17.5 |
| 7 | 3.5 | 6 | 3 | 24 |
| 8 | 4 | 7 | 3.5 | 31.5 |
| 9 | 4.5 | 8 | 4 | 40 |
| 10 | 5 | 9 | 4.5 | 49.5 |
| 11 | 5.5 | 10 | 5 | 60 |
| 12 | 6 | 11 | 5.5 | 71.5 |
The pattern will continue because one square is added to the horizontal or vertical length each time you turn a corner, so 1cm is added for each pair of vertical and horizontal strips.
However, we note that the vertical length is always 0.5cm less than the horizontal length, so 30cm x 24cm will not be possible with this particular way of making the mat.
Revisiting my initial assumptions, clearly the two about perfect fit of rope sections and 90 degree turns are idealisations of the perfect mat. In the real world, there will be gaps between rope sections (indeed, you can see them in the image) and angles will not be exactly 90 degrees. In terms of finding whether a particular size of mat is possible, I think the gaps are probably more significant. The other assumptions depend on these two, of course, but are otherwise reasonable, I think.
The final dimensions of the mat depend on:
- the length of the initial strip before the first turn
- where the coiling stops
Teachers' Resources
Why do this problem?
This problem provides a context from DT (designing an object for marketing) for formulating a mathematical model and investigating it. The investigation could be done by hand (as in the solution), or using a spreadsheet. More advanced students could be encouraged to use an algebraic approach.
Possible approach
A good place to start is by drawing the coils of rope on square paper. Doing this should lead to discussion about assumptions which need to be made, such as:
- a suitable diameter for the rope and length for the initial section of rope
- coils fit together without any gaps
- all sections of the coils are either horizontal or vertical
The drawing can then be used to investigate how the dimensions of the finished mat increase as additional sections or coils of rope are added - learners will need to decide whether they want to focus on the number of coils as each new rectangle is formed, or the number of sections of rope.
Key questions
- How does the length of the initial section of rope affect what finished dimensions are possible?
- How do the length and width increase with the number of coils or sections?
- Revisiting the initial assumptions, which do we think are reasonable, which are less so? How much do they affect our calculations?
Possible extension
Compare the analysis of rectangular mats with a circular mat constructed in a similar way. To compare which design is more economical requires finding the length of rope needed, to see which requires the least. This could be done by argument - that a circular mat of a given diameter will require less rope than a square mat of the same length. Alternatively the circular mat could be modelled as a series of concentric circles.
Possible support
Have rope or thick string available for learners to experiment with.
