Blue and White

We received correct solutions (that the areas were all the same) from:

• Charles Blackham (Shrewsbury House School)
• Michael Brooker (home educated),
• Andrei Lazanu (School number 205, Bucharest),
• Chong Ching Tong, Chen Wei Jian and Teo Seow Tian (River Valley High School, Singapore) and
• Chris Wells (Forres Academy).

Well done all of you.

I particularly liked Michael's solution because he generalised the result and I have used this as the basis of what follows. Although it was not intended to be a trick question Michael!

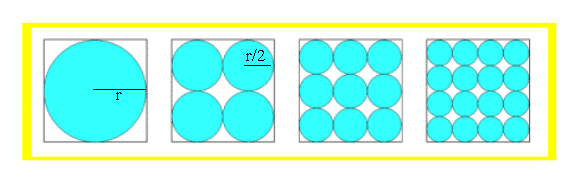
With one circle in the square the diameter is the length of one side of the square. The shaded area is ${\pi}{r^2}$ where $r$ = radius of the largest circle.

With four circles in the square, the diameter of one circle is half that of the large circle. The area of each small circle is ${\pi}({r/2}\: x \:{r/2})$. The total shaded area is $4({\pi}{r^2}/4)$. This can be simplified to ${\pi}{r^2}$. \par With nine circles in the square, the diameter of one circle is a third that of the large circle. The area of each small circle is $\pi(r/3\: x\: r/3)$. The total shaded area is $9({\pi}{r^2}/9)$. This can be simplified to ${\pi}{r^2}$.

We can go one step further by saying that with $n$ circles the area is $n({\pi}{r^2}/n)$ - which can again be simplified to ${\pi}{r^2}$. Therefore the answer is that the shaded area is the same in each picture.