Rhombicubocts
Problem
Image

|
Image
|
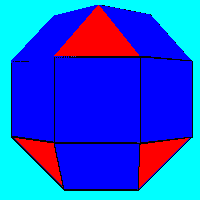
| Rhombicuboctahedron | Pseudo-rhombicuboctahedron |
Each of these solids is made up with 3 squares and a triangle around each vertex. Each has a total of 18 square faces and 8 faces that are equilateral triangles. Each has a band of 8 squares around the 'equator' and two square faces at the top and bottom (parallel to the equator) containing the 'north and south poles' at their centres. Draw the net for making each of the shapes and make the models for yourself either with card or a plastic constriction kit. How many faces, edges and vertices does each solid have? How many planes of symmetry and how many axes of rotational symmetry?
The solid on the left is one of the classical semi-regular or Archimedean solids but the one on the right was almost entirely ignored until it was made known by JCP Miller in the 1930s. Perhaps people thought the two were the same - can you describe the differences?
Student Solutions
Sandy from The Mount School, York, sent these nets for the solids and Jacqui from the same school sent similar nets. Each solid is made up of 18 squares and 8 equilateral triangles with 3 squares and a triangle around each vertex.

Sandy found that each solid has 48 edges, 24 vertices and 26 faces. It remains a Tough Nut Challenge to describe the differences between these two solids in terms of their planes of symmetry and axes of rotational symmetry.
To help with this you need a model. At the Mount School they use a method that is quick and easy for making models as this classroom picture shows (though it is not of rhombicubocts). The tabs slot together and you need to make the tabs narrow so they don't cover up much of the faces of the solid.

Alternatively you could use Polydron to make the models, or a similar construction kit with plastic pieces that clip together. With equipment of this sort you can make models quickly and use your time to concentrate on the mathematics.
