Parabolas Again
Problem
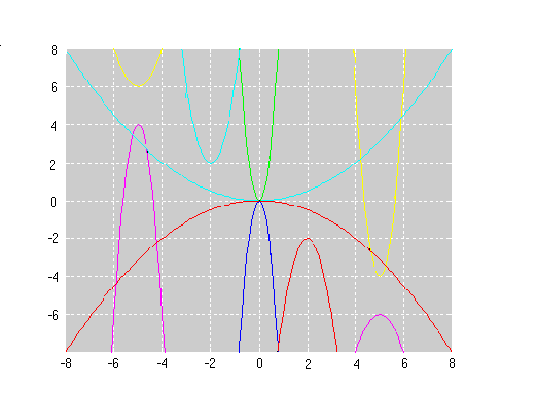
Here is a pattern for you to experiment with. This one is composed of the graphs of 14 parabolas. You may like to use a graphic calculator or graph drawing software to do this question.
The equations of three of the graphs are: $$y=2(x-6)^2-4$$ $$y=2x^2 -1$$ $$y= -2(x-4)^2 +3$$
Find the equations of the other 11 graphs in this pattern. Draw your own pattern and send it to us.
Getting Started
Student Solutions
This problem was solved by Ali Abu Hijleh, age 13, Alex Liao, age 14 and Prateek Mehrotra, age 14 from Riccarton High School, Christchurch, New Zealand and Andrei Lazanu, age: 12 from School No. 205, Bucharest, Romania. Well done all of you. This is Andrei's solution:
I observed that the equations of the parabolas given in the problem are of the form: $y = a(x + b)^2 + c$
where positive corresponds to parabolas with the opening towards the top, and negative to parabolas with the opening towards the bottom; are the coordinates of the peak. I identified the parabolas in your pattern and I verified them with the help of a small program in Matlab:
x=-8:0.1:8
y1=-2*(x+6).*(x+6)-2
y2=-2*(x+4).*(x+4)-1
y3=-2*(x+2).*(x+2);
y4=-2*x.*x+1;
y5=-2*(x-2).*(x-2)+2;
y6=-2*(x-4).*(x-4)+3;
y7=-2*(x-6).*(x-6)+4;
y8=2*(x+6).*(x+6)+2;
y9=2*(x+4).*(x+4)+1;
y10=2*(x+2).*(x+2);
y11=2*x.*x-1;
y12=2*(x-2).*(x-2)-2;
y13=2*(x-4).*(x-4)-3;
y14=2*(x-6).*(x-6)-4;
plot(x,y1,x,y2,x,y3,x,y4,x,y5,x,y6,x,y7,x,y8,x,y9,x,y10,x,y11,x,y12,x,y13,x,y14)
hold
axis([-8 8 -4 4]);
grid
Consequently, the equations of the 14 parabolas in your pattern are:
$y = -2(x + 6)^2 - 2$
$y = -2(x + 4)^2 - 1$
$y = -2(x + 2)^2$
$y = -2x^2 + 1$
$y = -2(x - 2)^2 + 2$
$y = -2(x - 4)^2 + 3$
$y = -2(x - 6)^2 + 4$
$y = 2(x + 6)^2 + 2$
$y = 2(x + 4)^2 + 1$
$y = 2(x + 2)^2$
$y = 2x^2 - 1$
$y = 2(x - 2)^2 - 2$
$y = 2(x - 4)^2 - 3$
$y = 2(x - 6)^2 - 4$
Andrei supplied the Matlab program but in order to challenge you to find his equations it is not reproduced here
Teachers' Resources

Here is another family of graphs sent in by Andrei from Rumania together with his solution to this problem. Can you find the equations of the graphs in Andrei's illustration?
These challenges, together with the two challenges Parabolic Patterns and More Parabolic Patterns , develop the ideas of transformations of graphs and the corresponding equations.
The illustrations give families of graphs, all of parabolas, formed by reflections in the $x$ and $y$ axes and in the line $y=x$, together with translations and stretches parallel to the axes.
You are not expected to plot and join points although it is helpful to consider where the graphs cut the axes. Rather you should think of the features of the graphs and the effects of the transformations.
