Bracelets
Investigate the different shaped bracelets you could make from 18 different spherical beads. How do they compare if you use 24 beads?
Problem
Well, in this country, and perhaps in yours, lots of young folk are wearing bracelets - both girls and boys. I was looking at some that my students wear and found that some were magnetic!
Many seem to have beads that are spherical and they go around the wrist quite comfortably. There are lots of different sizes and some have large beads and some quite small beads.
I suppose that most wrists are kind of oval - squashed circles - in shape and with the string or wire through the beads they fit very well.
It was playing with the magnetic beads off the person's wrist that gave me some ideas. There were $18$ beads altogether and they were all the same colour but I've chosen to show them in a variety of colours!
I found I could put them into different shapes:-
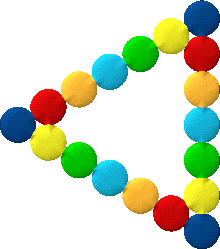
mind you, you'd have to have a triangular wrist for them to stay like that!
Now suppose we play around with this idea and make a rule that there has to be some shaped hole in the middle for a wrist. But we'll allow that to be all kinds of shapes :- vaguely triangular, rectangular, hexagonal etc.
You could try this out with marbles, circular counters, tiddly-winks, coins or with a drawing program on your computer.
I think we'll make a rule that the circles/spheres have to be the same size and you don't have to imagine that they're magnetic!
So here are some that I found with $18$ beads:-

I liked that one as it is the longest rectangle you could make - remembering to keep a wrist-hole. I then went on to:-

and then, almost a square :-

I like the next one - although it was a little hard to do on the computer!

Have a go at making these with your circles!
I then moved on to $24$ circles - it seemed to be a "good" number to choose - I wonder why?
I managed to get this regular shape:-

But then I thought that since I had $24$, perhaps I could make two that were exactly the same. So there's a new rule: You can make more than one bracelet as long as they're both the same.
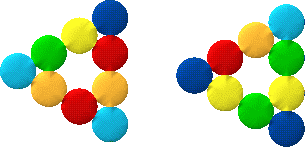
Have a go at using $24$ circles and make a large triangle and a fat square.
Well, now it's time to explore, to see what other bracelets you can make. Remember that there's to be a "wrist-hole". The shapes should be kind of "regular" but not strictly so, because then we could not use rectangles.
Other things to investigate:-
If you make a particular shape with $18$ and then the next size up comes when you use $24$, is there going to be the next size up at $30$?
So whatever shape you make, how many will you need to make the next size up? How does each shape grow? Look at the first shape I made using $24$:-
Image
What will the next size up of this look like?
- What are good numbers of beads to use? Why?
- What's the smallest number of beads that will allow you to make two identical bracelets? Why? How many will you need to make three of those?
If you make a bracelet with just one thickness of beads them how many will you need to make one that has a double thickness? Here's one I did by making the wrist-hole smaller and getting it to be twice as thick:
Image Image
Image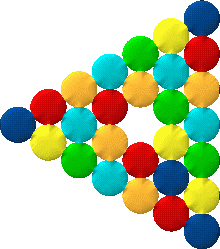
- Would cube beads lend themselves to exploring slightly differently? What about tetrahedral bead?
- What about ...?
Getting Started
Some dotted square or triangular paper would be useful.
You could use counters, cubes, anything instead of beads if you don't have them.
Student Solutions
We had some good ideas for Bracelets, here is a selection of ideas that were sent in.
First this was sent in by Fatima at the British School Al Khubairat in U.A.E.:
24 beads make an octagonal bracelet.
3 beads should be used on each side.
Alia and Fatima also from BSAK in U.A.E. sent in this good explanation of their ideas:
1. Yes because it has the same difference
2. 24 because it's even and in lots of times table like 8,3,4,6,2,12. You can make more irregular and regular shapes.
3. With 12 beads split up equally to make 6 for each bracelet. Make a triangle (2 on each side). And if we have 18 we can make 3 (still
triangular and still 2 on each side).
4. You make a square have 12 beads to use for the outside (3 on each side) then use 6 beads to fill the middle.
5. You can a square bead it will be a bit the same but straighter. A square-based pyramid bead; it would make it much more spikier.
6. What about a different bracelet? What about necklaces and rings? Using square-based pyramid beads you can have a spiky ring, necklace and
bracelet. And also we can make irregular bracelets.
Annabel and Anna from Norfolk House School said that to find out how many objects you'll need you take the amount of sides double it and add it on. So a square would go from 12 to 20 to 28.
Betsy from Mayfield Primary School wrote;
The smallest number of beads you can have for two bracelets is 10 unless you count the fact that with 8, 4 in each one there might be a space in the middle might not be depends on the way you draw it.
Another question I ask myself is what will happen if I'd have to make three bracelets. The smallest is 15 because with the numbers 14,13,12 and 11 you can not make three identical bracelets.
Other Questions: what will happen if you need to have the same amount of beads in 10 bracelets, what will be the smallest number?
What is the smallest number of beads you can have on one bracelet (with a hole in the middle)?
How many shapes can you make with 1-18,19-24, 25-48. 49-96, 97-etc.?
Thank you Betsy for those questions and thank you to the others from British School Al Khubairat for your work. We hope you had fun doing this.
Teachers' Resources
Why do this problem?
Possible approach

Key questions
Possible extension
Possible support
