The Big Cheese
Investigate the area of 'slices' cut off this cube of cheese. What would happen if you had different-sized block of cheese to start with?
Problem

I met up with some friends yesterday for lunch. On the table was a good big block of cheese. It looked rather like a cube. As the meal went on we started cutting off slices, but these got smaller and smaller! It got me thinking ...
What if the cheese cube was $5$ by $5$ by $5$ and each slice was always $1$ thick?
It wouldn't be fair on everyone else's lunch if I cut up the real cheese so I made a model out of multilink cubes:
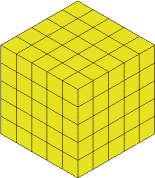
You could of course, just make $5$ slices but I wanted to have a go at something else - keeping what is left as close to being a cube as possible.
You can see that it's a $5$ by $5$ by $5$ because of the individual cubes, so the slices will have to be $1$ cube thick.
So let's take a slice off the right hand side, I've coloured it in so you can see which bit I'm talking about:
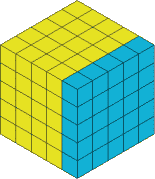
This now gets cut off and we have:
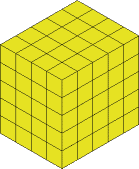
The next slice will be from the left hand side (shown in a different colour again):

Well the knife cuts and we are left with:

Remember I'm setting myself the task of cutting so that I am left with a shape as close to a cube shape as possible each time.
So the next cut is from the top. Hard to cut this so I would have put it on its side!

I'll remove that and I'm left with the $4$ by $4$ by $4$ cube
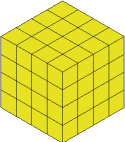
I do three more cuts to get to the $3$ by $3$ by $3$ and these leave the block like this:



I'm sure you've got the idea now so I don't need to talk as much about what I did:



and then onto:
That leaves you with two of the smallest size cube $1$ by $1$ by $1$.
If we keep all the slices and the last little cube, we will have pieces that look like (seen from above):
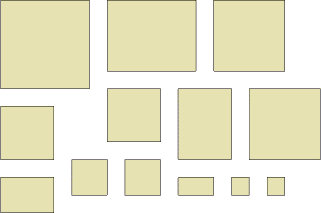
C H A L L E N G E
Now we have thirteen objects to explore.
- What about the areas of these as seen from above?
- What about the total surface areas of these?
- What about their volumes of the pieces?
A L S O
Investigate sharing these thirteen pieces out so that everyone gets an equal share.
What about ...?
I guess that once you've explored the pattern of numbers you'll be able to extend it as if you had started with a $10$ by $10$ by $10$ cube of cheese.
Getting Started
You could make a note of the area of each piece as seen from above, and group them according to the cube that you started with i.e. in threes. This might help you notice some patterns to investigate. What happens if you add in these groups?
You could look at the difference in size of successive pieces.
Student Solutions
Chloe, Emily, Rebecca, Scarlett, Chloe, Alana, Isobel, Shauna and Joel from Griffithstown Primary School sent in various solutions that were all very interesting and showed hard work. Here is a summary taken from their suggestions.
I found out that we can share the $13$ slices of the big cheese between $5$ people. This is how we did it:
The first person had a slice of cheese that was $25$cm$^2$.
The second person had $3$ slices of cheese that was $20$cm$^2$ + $4$cm$^2$ + $1$cm$^2$ = $25$cm$^2$.
The third person had $5$ slices of cheese that was $12$cm$^2$ + $6$cm$^2$ + $4$cm$^2$ + $2$cm$^2$ + $1$cm$^2$= $25$cm$^2$.
The fourth person had $2$ slices of cheese that was $16$cm$^2$ + $9$cm$^2$ = $25$cm$^2$.
The fifth person had $2$ slices of cheese that was $16$cm$^2$ + $9$cm$^2$ = $25$cm$^2$.
So everybody had an equal share of cheese but in different sizes.
The children at Mayfield Primary School in the UK found the same solution, and used Cuisenaire rods to represent the slices of cheese:

Can you see how each of these slices has been cut from the large piece? You might like to have a look at Mayfield Primary School's full solution to see how they made each of these slices.
Cherian from Quarry Bay School sent in the following;
Solution for the third investigation for The Big Cheese. My solution:
First you imagine the two $1$ by $1$ by $1$ cubes put on top of each other.
Then you put the $1$ by $1$ by $2$ layer beside the other one.
After that, put another $1$ by $1$ by $2$ layer in front of it, so that you will have a $2$ by $2$ by $2$ cube.
Now you have to put $2$ by $2$ by $1$ layer on top of it.
Then you put $2$ by $3$ by $1$ layer on the left side.
After that you put a $3$ by $3$ by $1$ layer behind it.
Then you put another one on your cube.
Now you put a $3$ by $4$ by $1$ layer beside it.
Then put a $4$ by $4$ by $1$ layer behind it.
Now you have a $4$ by $4$ by $4$ cube.
After that you put a $4$ by $4$ by $4$ layer on top of it.
Then put a $4$ by $5$ by $1$ layer beside it.
Now put a $5$ by $5$ by $5$ layer behind it, so now you have a $5$ by $5$ by $5$ cube!!
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
For more extension work
This pupil could be presented with the same idea as using a $5$ by $5$ by $5$ piece of cheese but consider using a knife to carefully cut cubes from it. I would set the challenge to find all the different ways of cutting cubes (with as little waste as possible) from it. For example you can obviously cut $125$ cubes of size $1$ - so that's one way. Can you cut it to produce some other size as well as $1$'s? So, how many ways altogether?
Possible support

