More Parabolic Patterns
Problem
The illustration shows the graphs of twelve functions. Three of them have equations
$y = x^2$
$x = y^2$
$x = -y^2 + 2$
Use a graphic calculator or a graph drawing program to sketch these three graphs and then to locate them in this illustration. Use the clues given in this information to help you to find the equations of all the other graphs and to draw the pattern of 12 graphs for yourself. For your solution send in the equations you have found with an explanation of how you did it.
Getting Started
Sketch the graphof $y=x^2$. If you exchange $x$ and $y$ the point $(a,b)$ on one graph has an image $(b,a)$ on the other graph. What transformation of the graphs will have this effect? What do you expect the graph of $x= y^2$ to look like? Find these two graphs on the illustration.
Now use a graphic calculator, or graphing software, to sketch the two graphs. Were your predictions correct?
Find the other equations by considering the transformations of the graphs, changing the equations accordingly and testing your decisions by sketching the graphs and seeing if they match the graphs in the illustration in the way that you expected.
Student Solutions
We have received solutions from Sarah (Madras College, St Andrews), Andrei (School no. 205, Bucharest, Romania) and from Ryan and Belinda (Riccarton High School, Christchurch, New Zealand). Well done to you all.
All approached the problem in a similar way. Ryan and Belinda's response follows:
To get the lines curving downward from the top
We are given the equation for the middle curve (that goes through the point $(0,0)$) which is $y=x^2$. From there we add or subtract $2$ to give the curves going through the points $(0,2)$ and $(0,-2)$ respectively, giving the equations -

To get the lines curving upward from the bottom
This is a reflection of the downward curves, so we use opposite equations, e.g. instead of $y=x^2$we use $y=-x^2$. From there we add or subtract $2$ to give the curves going through the points $(0,2)$ and $(0,-2)$ respectively, giving the equations -
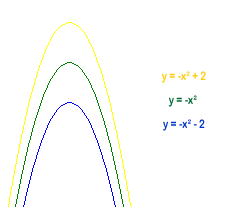
To get the lines curving from right to left
We are given the equation for the middle curve (that goes through the point $(0,0)$) which is $x=y^2$. From there we add or subtract $2$ to give the curves going through the points $(2,0)$ and $(-2,0)$ respectively, giving the equations -
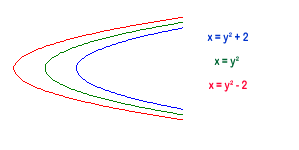
To get the lines curving from left to right
This is a reflection of the right to left curves, so we use opposite equations, e.g. instead of $x=y^2$we use $x=-y^2$. From there we add or subtract $2$ to give the curves going through the points $(2,0)$ and $(-2,0)$ respectively, giving the equations -

Teachers' Resources
This is another inverse problem. If you were given the equations and asked to draw the graphs then graphing software would do the work for you. This challenge is posed the opposite way round. You have to use mathematical reasoning to deduce the equations of the graphs in the illustration. Then you can use graphing software to check to see if your reasoning was correct.
