Filling the Gaps
Which numbers can we write as a sum of square numbers?
Problem
Filling the Gaps printable sheet
Charlie has been thinking about which numbers can be written as a sum of two square numbers. He took a $10\times10$ grid, and shaded the square numbers in blue and the sums of two squares in yellow.
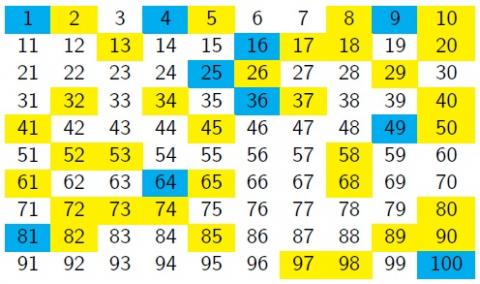
He hoped to find a pattern, but couldn't see anything obvious.
Vicky suggested changing the number of columns in the grid, so they reduced it by one:
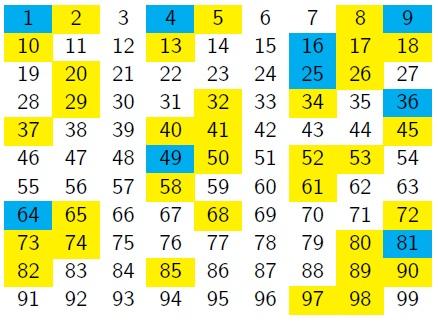
"There seems to be a diagonal pattern."
"If the rows were one shorter, then those diagonals would line up into vertical columns, wouldn't they?"
"Let's try it..."
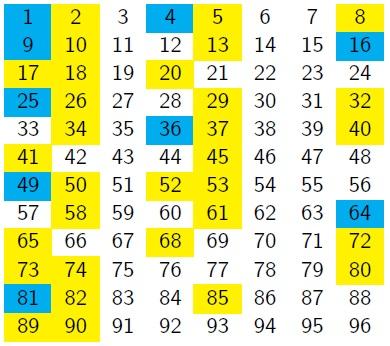
What do you notice about the positions of the square numbers?
What do you notice about the positions of the sums of two square numbers?
Can you make any conjectures about the columns in which squares, and sums of two squares, would appear if the grid continued beyond 96?
Can you prove any of your conjectures?
You might like to look back at the nine-column grid and ask yourself the same questions.
Charlie couldn't write every number as a sum of two squares. He wondered what would happen if he allowed himself three squares.
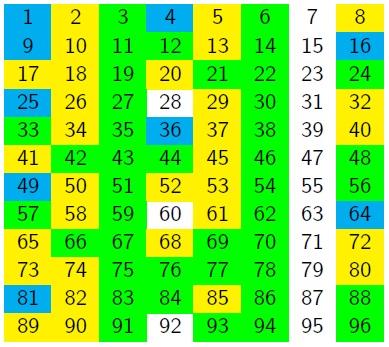
Will any of the numbers in the seventh column be a sum of three squares?
Can you prove it?
"We must be able to write every number if we are allowed to include sums of four squares!"
"Yes, but it's not easy to prove. Several great mathematicians worked on it over a long period before Lagrange gave the first proof in 1770."
With thanks to Vicky Neale who created this task in collaboration with NRICH.
Getting Started
It may be helpful to look at the problem What Numbers Can We Make?
In which columns do the square numbers appear?
In which columns do the squares of even numbers appear? Can you explain why?
And the squares of odd numbers? Can you explain why?
How can we describe the numbers in a particular column?
You might want to start by looking at the completely empty columns.
Student Solutions
Well done to Christopher from Sale Grammar School who sent us this solution using modular arithmetic.
Teachers' Resources
Why do this problem?
This problem provides an interesting context in which students can apply algebraic techniques and ideas about modular arithmetic. It also gives them a taste of an area of number theory that they might study if they go beyond the school curriculum.
Possible approaches
This problem follows on nicely from What Numbers Can We Make?
Possible support
Ensure that students have worked on What Numbers Can We Make?
Possible extension
Suggest that students look for patterns that they can explain in the nine-column grid.
