Where Can We Visit?
Charlie and Abi put a counter on 42. They wondered if they could visit all the other numbers on their 1-100 board, moving the counter using just these two operations: x2 and -5. What do you think?
Problem
Where Can We Visit? printable sheet
Here is a 100 square board with a counter on 42:

Using either of the two operations $\times 2$ and $-5$, whereabouts on the 100 square is it possible to visit?
You might start like this: $$42, 37, 32, 27, 22, 17, 12, 7, 14, 9, 18, 13, 26, 52, 47, 42, 84 ...$$Notice that you are allowed to visit numbers more than once.

Is it possible to visit every number on the grid?
What if you start on a different number?
Can you explain your results?
Choose pairs of operations of your own and investigate what numbers can be visited.
You might like to print off some 100 squares.
Is there a way to predict which numbers it's possible to visit, for a given starting point and a pair of multiplication/subtraction operations?
This problem is also available in French: Où Irons-nous?
Getting Started
What happens to multiples of 5 when they are doubled?
What about numbers that are 1 more, 2 more, 3 more and 4 more than a multiple of 5?
What happens to multiples of 5 when 5 is subtracted from them?
What about numbers that are 1 more, 2 more, 3 more and 4 more than a multiple of 5?
Student Solutions
Fantastic responses to this problem, Benjamin and George discovered this:
We started with 42 and using the rule multiply by 2 and subtract by 5.
We discovered when any number with the factor of 2 is doubled (multiplied by 2) it gives a units digit of 4, 8, 6, and back to 2 which we started with. Although you can get round this by subtracting 5 it only then takes you to 7, 3 1 and 9 which with the 10 by 10 grid it becomes impossible to numbers with the factors or multiples of 5 e.g. 5, 10 15...
Lydia and Jess explain their findings:
Lyman Shen explored other combinations of multiplying and subtracting:
When the start number ends with 5 or 0, there are no way to get any number that ends in anything other than 0 and 5.
Teachers' Resources
Why do this problem?
This problem offers all students opportunities to explore fundamental ideas about number theory in a simple context. They are encouraged to explore, conjecture, generalise and justify. There are opportunities for older students who are familiar with algebraic manipulation or modulo arithmetic to produce rigorous proofs.
Possible approach
You need a set of number cards 1-100, with the multiples of 5 removed. Shuffle the cards in front of the class and hand out one to each student. Do not tell them that the multiples of 5 are missing!
21, double, 42, take five, 37, take five, 32, take five, 27, double, 54
Finally challenge the class to get to your number (which should be a carefully chosen multiple of five). You may wish to offer a prize......
Once the class give up, ask them to explain why it is impossible.
Demonstrate how the numbers are crossed out as they are visited.
Can they explain their findings and use these to begin to make predictions about other pairs of operations? Encourage them to justify their predictions.
You might find it useful to see if they can identify the pair of operations that produced the patterns in the three grids below. They can choose from either:
$\times 3$ and $-6$,
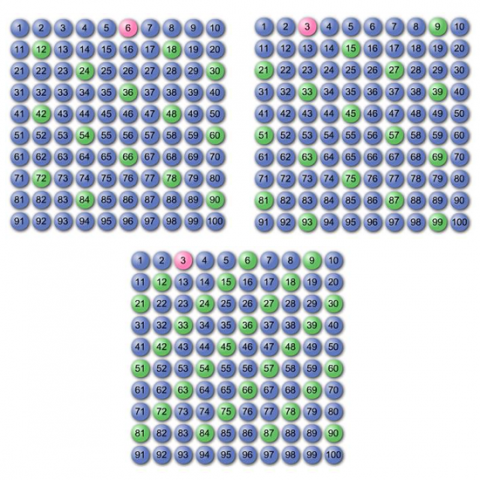
Key questions
What happens to multiples of 5 when they are doubled?
What happens to multiples of 5 when 5 is subtracted from them?
What about numbers that are 1 more, 2 more, 3 more and 4 more than a multiple of 5?
Possible support
Most students will have little difficulty with doubling or subtracting 5, but may find it more difficult to spot the patterns involved. Using coloured arrows to represent repeated subtractions of 5 on various 1-100 grids (each starting from a different number) may help them to see the patterns emerge.
Possible extension
Students may be interested in this introductory reading on Modular Arithmetic.
Students could have a go at Take Three from Five which has a similar underlying structure. Can they use their insights from the previous problem to solve this challenge?
