Any Win for Tennis?
Problem
A mathematician tennis player said:
"In tennis you win a game if you score 4 points before your opponent scores 3 points. Or, if you both score 3 points at some stage you win if you manage to score 2 points in a row after the 3-all stage before your opponent does."
This sentence is quite a mouthful to say, so first think about what it means! If you play tennis, think about how this mathematically represents the scoring system.
Suppose that you have a fixed chance of $0.6$ of winning any given point. What is your chance of winning a game?
Numerical extension
In reality a fixed chance of winning a point is not a good assumption. Suppose that Ahmed has a 60% chance of winning the first point if he serves, 80% chance of winning a point if he has just won a point and a 40% chance of winning a point if he has just lost a point. Suppose that Bryoni's chances are 85%, 80% and 30% respectively if she serves.
What chance would each player have of winning a service match?
Explore.
In the 2010 Wimbledon Championships, Isner and Mahut played the longest match in tennis history: the match went on for three days and finished with a score of 70-68! (You can read about it in the Plus article here) After the match, Isner said that a match like this will never happen again.
I wonder if Isner was correct in this statement. The famous Cambridge mathematician Tim Gowers thought about this question on his blog.
Getting Started
Consider the difference between games which hit 3 points each and those which don't.
Note that some sequences of games occur with the same probability as others (e.g. LWWWW and WLWWW).
For the numerical parts, you will need to decide the accuracy to which you wish to compute the answers. You might like to verify numerically any answer that you make to the first part of the question.
Student Solutions
Steve writes
Once I had understood the scoring systems I realised that I needed to look at the chances of winning based on whether I reached deuce or not. Let $V$ be the event of victory in the the overall game and $D$ the event of reaching deuce ($3$ points all) and $P_0, P_1$ and$P_2$ the probability of winning the game whilst losing $0$, $1$ and $2$ points respectively.
$$P(V) = P_0+P_1+P_2+ P(V|D)P(D)$$
$P_0, P_1$ and$P_2$ correspond to games of $4$, $5$ and $6$ points respectively. Each of these must end in a winning point (denoted W). The number of such games equals the number of ways of distributing $0$, $1$ and $2$ lost points (denoted L) amongst $3$, $4$ and $5$ points. The game reaches deuce if $6$ points are played with $3$ $W$s and $3$ $L$s. The number of such games equals the number of ways of distributing $3$ $L$s into $6$ points. Since each point is won or lost independently of the other points the probabilities multiply. Therefore,
$$P(V) = (0.6)^4\cdot 1 + (0.6)^4(0.4)\cdot 4 + (0.6)^4(0.4)^2\cdot \frac{5\cdot 4}{2}+P(V|D)\cdot(0.6)^3(0.4)^3\cdot\frac{6\cdot 5\cdot 4}{3\cdot 2}$$
I now need to use conditional probability to work out the chance of winning given that I reach deuce
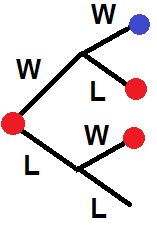
The red dots on this tree indicate branches where the probability of winning equals the probability of winning given that I am at deuce $P(V|D)$ and the blue dot is a victory $V$.
$$P(V|D) = (0.6)^2 + (0.6)(0.4)P(V|D)+(0.4)(0.6)P(V|D)$$
which can be rearranged to
$$P(V|D) = \frac{(0.6)^2}{1-2(0.6)(0.4)}$$
Putting all of this together yields a probability of victory of
$$P(V) =(0.6)^4\left[ 1+ 4(0.4)+10(0.4)^2\right] +\frac{20(0.6)^5(0.4)^3}{1-2(0.6)(0.4)}$$
This equals $0.736$ (3dp). I left the probabilities in so that I could check the calculation by replacing the $0.6$ and $0.4$ by $0.5$. In this case, I get $0.5$, which makes sense (even players have an even chance of winning in this set of game rules). I also get a guaranteed victory by changing the $0.6$ to $1$ and setting the $0.4$ to $0$, which also makes sense (you will win if you win every point!)
--------------
For the second part of the problem I used a spreadsheet. It was inefficient, but displayed the probabilities clearly. After a bit of thought it is clear that the $P(V|D)$ depends on whether deuce was reached on a $W$ or on a $L$. I'll need two new events $D_W$ and $D_L$ for these cases.
We now have
$$P(V)= P(V|\bar{D})P(\bar{D})+P(V|D_L)P(D_L)+P(V|D_W)P(D_W)$$
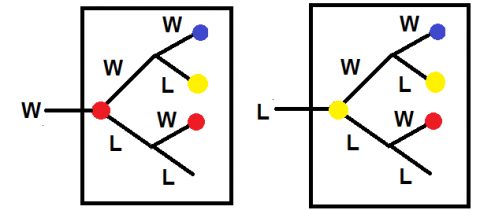
There is a fun pair of linked trees for the $P(V|D)$ - in the diagram the red circles represent $P(V|D_W)$ and the yellow circles represent $P(V|D_L)$. Reading off the probabilities gives a pair of simultaneous equations:
$$P(V|D_W) = (0.8)^2+(0.8)(0.2)P(V|D_L)+(0.2)(0.4)P(V|D_W)$$
$$P(V|D_L)=(0.4)(0.8)+(0.4)(0.2)P(V|D_L)+(0.6)(0.4)P(V|D_W)$$
This gives $P(V|D_W) = 0.792$ (exact value $\frac{80}{101}$) and $P(V|D_L) = 0.554$ (exact value $\frac{56}{101}$)
Using this piece of conditional probability to simplify the numerical analysis I then used a spreadsheet (Tennis.xls ) to calculate that
$$P(D_L) = 0.0755, \quad P(D_W) = 0.0947$$
Using this I calculate the chance of victory as
$$P(V) = 0.7364$$
For Bryony the numbers are
$$\begin{eqnarray}P(V|D_W) = 0.753\\P_(V|D_L)= 0.423\\P(D_L) = 0.0857\\P(D_W)= 0.0646\\P(V) =0.7383\end{eqnarray}$$
So, the players are very evenly matched.
You can check the results on this spreadsheet: Tennis.xls
Teachers' Resources
Why do this problem?
This is an interesting and complicated scenario which will require clear probabilistic thinking. There will be various different ways in which the first part of the problem can be attempted, and it would be informative to compare and contrast these. It is quite a difficult problem and could be set to keen students individually or discussed collectively. It would be good as revision of a module on probability or to motivate the advanced study of probability.
Possible approach
- There are different sorts of winning sequences, such as WWWLW, WWLLW.
- Each winning sequence ends with a W.
- There are arbitrarily long winning sequences WWWLLL(WL)....(WL)WW.
- Not all winning sequences are of the same probability.
Key questions
Possible extension
Possible support
