Train Carriages
Problem
I was on a train the other day and I was looking out of the window as we went through a station and I saw lots and lots of carriages waiting in another line. They were going to be linked together to make a new train going on a long journey - so I thought !!
It was then that my train went round a curve in the track and I looked out of the window and saw the front of my train and quickly turned my head and saw the back of the train.
After a few more miles I had seen that my train had ten carriages to make up the whole train.
![]()
I thought back about the carriages I had seen at the station and wondered about making them into several trains.

I thought my train was rather special having ten carriages so I want to put this challenge to you all.
- Suppose there are $24$ carriages.
- They're going to be put together to make up some trains.
- The smallest train you are allowed is one with two carriages.
- You must include at least one "ten-carriage train".
That's all really.
Here are some to start you off.

You could draw these.
You could use cubes/ beads/ boxes or whatever to stand for the
carriages. So it might also look like:-
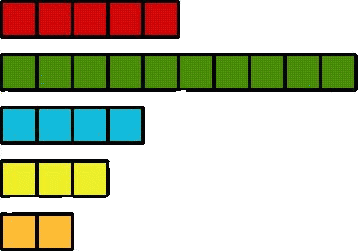
Next:-

and if you used squares or cubes it might look like:-
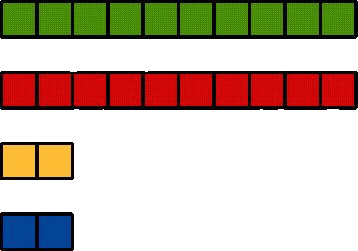
So now it's your turn. See what different train arrangements you can make.
Remember the four "Rules" above.
It would be good to think if you have been using some kind of special way of getting new ones. Maybe you've found a pattern that helps you get lots of answers?
Please write to us and tell us about your ways of doing this.
FINALLY
You simply have to ask "I WONDER WHAT WOULD HAPPEN IF ...?"
Here are some to start you off.
"I wonder what would happen if I had to only make
three trains?"
"I wonder what would happen if I had to make only
four trains?"
"I wonder what would happen if I had to have all the trains
different lengths?"
and so on
and so on
and so on.
Student Solutions
There are lots of answers to this problem, depending on what questions you choose to ask.
Have a go yourself, and if you discover anything interesting,e-mail us to tell us what you've done! Please don't worry that your solution is not "complete" - we'd like to hear about anything you have tried. Teachers - you might like to send in a summary of your children's work.
