The Add and Take-away Path
Two children made up a game as they walked along the garden paths. Can you find out their scores? Can you find some paths of your own?
Problem
The Add and Take-away Path printable sheet
Once there was a garden with lots of paths and little patches of grass between them. It looked a bit like this:

Two children, William and Thea, made up a game.
For every patch of grass they passed as they walked to the right on the picture, they added one.
For every patch of grass they passed as they walked to the left on the picture, they took away one.
If they went North (up on the picture), they added two for every patch of grass, and if they went South (down on the picture), they took away two for each patch of grass.
They started with ten points at S, and added and took away until they reached E.

These are the paths they took:

Thea took the yellow path. Remember she started with $10$ points.
How many points did she have when she arrived at E?
William took the purple path.
How many points did he have when he arrived at E?
In the picture below, we've taken out the grass and just drawn a grid. You can imagine that the squares are patches of grass and the lines are the paths in the garden.
We have marked different starting and end points.
What would your score be if you walked along the blue path?
And the red path?
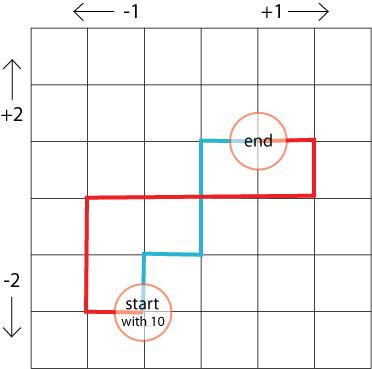
Make up some more paths between these start and end points.
What is your score each time?
What do you notice?
Can you explain why?
You might like to print off a copy of the grid to work on.
Getting Started
Try it out!
You could start with $10$ counters and add more or take them away as you move along your path. Then, when you reach the end of the path, you can count the number of counters you have left to find out your score.
How will you make sure you remember the paths you've tried?
How will you remember the score each time?
Student Solutions
Jack from Heacham Infant and Nursery School looked at Thea's and William's routes and told us:
The score each time was $16$.
It did not matter which route you take, the score was the same.
Ellie from Short Wood Primary School looked at the red and blue routes. She said:
the red path takes the route of:
minus $1$, plus $2$, plus $2$ , plus $1$, plus $1$, plus $1$, plus $1$, plus $2$, minus $1$ which will give you a total score of $18$ points
the blue path takes the route of:
plus $2$, plus $1$, plus $2$, plus $2$, plus $1$ which will give you the score of $18$ points
So the solution is that if you take the longer red path you will score exactly the same as the shorter blue path.
David from Belmont Primary School began to explain why these two routes gave the same total:
The reason that it is impossible to get any other number than $18$ is because the shortest path from start to finish is $2$ right and $3$ upwards, leaving you with $18$ ($10+1+1+2+2+2$). Therefore, any other move to attempt getting less points by subtracting (moving left/down) would be met by an equal addition of the same number (moving right/upward). So ultimately any path (no matter how complex) would lead to $18$.
Someome from St Matthew's gave a good explanation too:
I conjecture that the line you draw can be of any length.
The quickest way to get from start to finish is in $5$ moves and this adds up to $18$ (starting with $10$).
If you imagine that your line is a brick wall and you make an extension in the middle of it, then as you move backwards and forwards, the operations always cancel each other out. E.g. if you move up $1$, you add $2$ and then if you move down $1$, you take away $2$. Whatever shapes you make it doesn't matter because the moves always cancel each other out.
Well done!
Teachers' Resources
Why do this problem?
This problem will give children a chance to generalise and make predictions. It also provides practice in simple addition and subtraction. It draws out the inverse relationship between these two operations as well as encouraging children to think about the order of operations.
Possible approach
You could start by showing the pictures in the first part of the problem to the whole group, making sure that William and Thea's game is understood. A small scale version could be drawn out on the playground or on the hall floor so that the game can be played practically.
Key questions
Possible extension
Possible support
Learners might find it useful to have counters to help keep track of the score. Starting with $10$ counters, they could physically add and take away counters, then count them up when they arrive at the end point.
