Population Dynamics - Part 5
Problem
The Lotka-Volterra Equations
The Lotka-Volterra equations allow us to model a biological system containing a predator and a prey species. They arose in the 1920s due to the independent work of the mathematicians Alfred Lotka and Vito Volterra.
Formulating the Equations
Let x be the size of a fish population and y be the size of the shark population. If the prey have an unlimited food supply and no predators, then they grow exponentially according to the equation $\frac {\mathrm{d}x}{\mathrm{d}t}=\lambda x$ , for some constant $\lambda$.
If there are more sharks, more fish will be killed and if there are fewer sharks, then fewer fish will be killed. So the rate of predation upon the prey is proportional to the rate at which the predators and prey meet. We represent this by $\alpha xy$.
Note that if either x or y is zero then there can be no predation.
The equation for prey becomes: $$\frac {\mathrm{d}x}{\mathrm{d}t}=\lambda x-\alpha xy =x(\lambda -\alpha y)$$ Conversely, predators rely on prey to survive, so in the absence of any prey, the predator equation is $\frac {\mathrm{d}y}{\mathrm{d}t}=-\gamma y$. The growth of the predator population will depend on the population sizes of the predators and prey, and the ability of the predators to successfully catch prey. We represent this by $\beta xy$.
The equation for predators becomes: $$\frac {\mathrm{d}y}{\mathrm{d}t}=\beta xy-\gamma y =y(\beta x -\gamma)$$
Using the Equations
We are interested in population equilibrium, which occurs when neither population is changing: $$ \begin{align*} \frac {\mathrm{d}x}{\mathrm{d}t}&=\frac {\mathrm{d}y}{\mathrm{d}t}=0 \\ x(\lambda -\alpha y)&=y(\beta x -\gamma)=0 \\ \Rightarrow x=0,y=0 &\text{ and } x=\frac{\gamma}{\beta}, y=\frac{\lambda}{\alpha} \end{align*}$$ The first solution occurs when both species die out, the second when the sizes of both species reach an equilibrium with each other.
Determining the stability of these equations, requires knowledge of the Jacobian matrix and linearization, which we exclude for complexity.
Question: Consider a species of fish, x, and a species of shark, y, with population equations: $$\frac {\mathrm{d}x}{\mathrm{d}t}=2x-4xy , \frac {\mathrm{d}y}{\mathrm{d}t}=xy-2y$$ a) Where are the equilibrium points?
b) Below is a phasor diagram of the above equations. Try and work out what it is representing. What happens at the red point?
We can also plot the size of the populations against time on the same graph. The graph below clearly shows the dependency of the shark population on a large population of prey, and the oscillatory nature of the two population sizes.
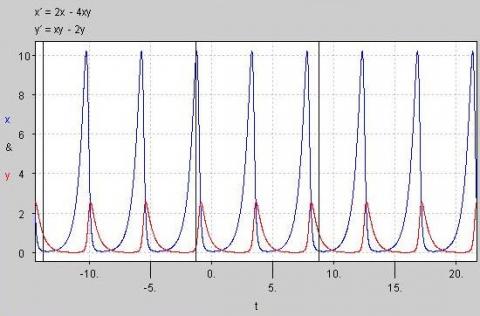
Question: Why do you think the shark population peaks after the fish population has soared? Why do you think the shark population is always less than the fish population?
Limitations to our model
In reality if two species coexist, their interactions also depend on the environment they inhabit. This is explored further here. Some of the assumptions made in the above equations are:
- The prey always find ample food
- The rate of change of population is proportional to its size
Question: Can you think of any other assumptions we have made in our model?
Getting Started
Although there is no 'right' answer to an estimation, there are good or bad estimations and sensible or over detailed calculations.
Think how you might make your estimation a good one, and think how it makes sense to ignore certain complexities in the calculation.
Student Solutions
Red dot is when the populations of sharks and fish will remain unchanged.
the equilibrium points are $x=y=0$ and $x=2, y=0.5$
Other factors
- The predators only get food by eating the prey
- The environment does not change to favour one species and genetic evolution is slow
Teachers' Resources
Why do this problem ?
Practice with the use of numbers is a crucial biological skill. These interesting questions will allow you to practise these skills whilst developing awareness of orders of magnitude in scientific contexts.Possible approach
There are several parts to this question. The individual pieces could be used as starters or filler activities for students who finish classwork early. Enthusiastic students might work through them in their own time. Since there is no absolutely 'correct' answer to many of these questions, they might productively be used for discussion: students create their own answers and then explain them to the rest of the class. Does the class agree? Disagree? Is there an obvious best 'collective' answer?Key questions
- What assumptions will you need to make in this question?
- How accurate do you think you answer is?
- What order of magnitude checks could you make to test that your answer is sensible?
