Walkabout
Problem
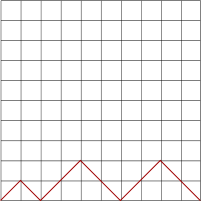
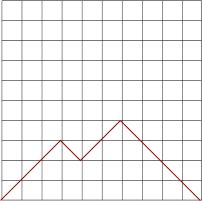
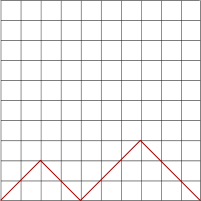
A walk is made up of diagonal steps, starting at the bottom left and ending up back on the bottom line (x-axis). You can move diagonally up and down towards the right but you cannot move towards the left.
A diagonal must go from a left-hand corner of a square to the opposite right-hand corner of the same square.
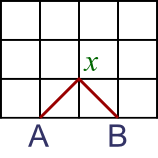
The examples above all show 10-step walks. So let's look at a 2-step walk in more detail:
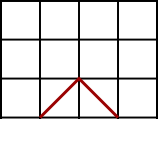
There is only one way to make a 2-step walk - from A up to x and down to B:
Here are two 4-step walks:
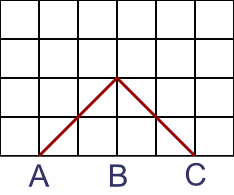
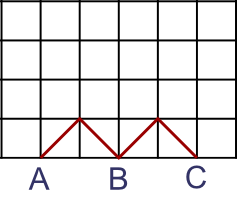
Are there any more 4-step walks?
How do you know you have them all?
How many 6-step, 8-step walks are there?
Can you find a general rule?
See also the problems One Basket and Counting Binary Ops
Getting Started
The 'trick' is finding a systematic way to record all possibilities.
Student Solutions
This one was a tough problem! Some of you started to spot patterns and suggested possible rules, but the patterns didn't continue. In fact, a general rule for this sequence is pretty hard to write down! One very useful way of recording the number of walks of up to eight steps was this:
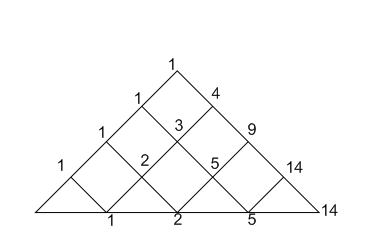
Can you see how the diagram works? Could you continue it to find the number of ten-step walks?
Teachers' Resources
Why do this problem
Possible approach
Key Questions
- Can you describe what is the same about the two problems that might explain the similar mathematical structure?
- What is different about and what is similar to other examples, such as One Step Two Step and Room Doubling that result in a Fibonacci sequence?
Possible support
Group photo can be done with real people and you can start with small numbers. Spend plenty of time trying out, and considering the efficiency of, possible recording methods.Possible extension
Can students make connections between the structures of the two problems that may in part explain the mathematical connections?Notes
$ 1$, $ 1$, $ 2$, $ 5$, $ 14$, $ 42$, $ 132$, $ 429$, $ 1430$, $ 4862$ ,...
The Catalan numbers describe things such as:
- the number of ways a polygon with n+2 sides can be cut into n triangles
- the number of ways to use n rectangles to tile a stairstep shape (1, 2, ..., n-1, n)
- the number of ways in which parentheses can be placed in a sequence of numbers to be multiplied, two at a time
- the number of planar binary trees with n+1 leaves
- the number of paths of length 2n through an n-by-n grid that do not rise above the main diagonal
The Catalan numbers are also generated by the recurrence relation:
$ C_0=1, \qquad C_n=\sum_{i=0}^{n-1} C_i C_{n-1-i}.$
For example, $ C_3=1\cdot 2+ 1\cdot 1+2\cdot 1=5$, $ C_4 = 1\cdot 5 + 1\cdot 2 + 2\cdot 1 + 5\cdot 1 = 14$, etc.
