Paint rollers for frieze patterns
Image
Tile pattern from Palacio de Velazquez, Parque de Retiro, Madrid, Spain
Frieze patterns are formed by repeating copies of one small bit of the pattern (the motif) over and over again by translation, rotation and reflection. The identification of the symmetries in the pattern (the transformations which map the pattern into itself) is independent of the motif. All frieze patterns involve translations in one direction only and patterns involving translations in two directions are called wallpaper patterns. Classification of these symmetries using group theory shows that there are exactly seven frieze patterns and seventeen wallpaper patterns.
This article provides an introduction to the classification of frieze patterns by reducing the problem to studying the symmetries of a cylinder. It will be an advantage if you have never met frieze groups but in any case pause now and think about all the symmetries of a cylinder that you can visualise.
It is intuitively obvious that the cylinder can be used as a paint roller so that if a pattern is embossed on it, the pattern can be transferred to paper by repeating it over and over again in a strip with each revolution of the cylinder. Conversely, given a frieze pattern on a piece of paper one can wrap the paper around a cylinder of a suitable radius in such a way that the pattern is produced once and only once on the cylinder. For the purposes of this work we consider symmetries of the cylinder other than those involving rotations about the axis of the cylinder which would correspond to the frieze pattern being copied more than once on the surface of the cylinder. | Image
|
| Frieze patterns and wallpaper patterns occur in the art of many cultures and there is often evidence of exploration of the different possible symmetries. Escher's work was influenced by the frieze and wallpaper patterns he saw on a visit to The Alhambra in Granada, Spain. Some Japanese patterns have to be matched in pairs in one of the NRICH challenges, an NRICH article investigates frieze patterns in car tracks and here is an article by Heather McLeay on frieze groups illustrated by her photos of cast iron railings taken all over the world. | Image
Photo by Heather McLeay |
The Frieze Tree article provides a systematic way to distinguish one frieze group from another.
We are going to illustrate the seven frieze groups using patterns on a cylinder. With only one footprint on the cylinder the patterned cylinder can only be mapped to itself by the identity transformation $I$. This is the simplest frieze group and the corresponding frieze pattern is made up of repetitions of one footprint as if made by someone hopping along.
Image
|
With the footstep pattern on the cylinder shown here the only symmetries are the identity transformation and reflection in a plane containing the axis of the cylinder. Suppose you denote this reflection by $Y$ then $Y^2=I$ and the group is $\{I, Y\}$.The group operation for all the groups referred to in this article is combination of the transformations and for simplicity we simply refer to the groups by giving the set of elements.
|
Imagine printing a frieze pattern using this cylinder as a paint roller and compare the pattern to the frieze at the top of this article. Of course there are infinitely many other groups consisting of the identity and one reflection in a vertical plane through the axis of the cylinder but because they all have an identical structure (isomorphic groups) we classify them as one type.
A set of symmetries of an object becomes a group when the set contains all the combinations of symmetries within the set. We aim to find all the groups of symmetries of the cylinder other than the infinitely many groups involving rotations about the axis of the cylinder.This is a similar challenge to Rose which you may like to try before proceeding.
Ignoring rotations about the axis of the cylinder, before you read on, draw other patterns on cylinders to show different sets of transformations that map the 'patterned' cylinder onto itself. Each time list all the symmetries (rotations, reflections and glide reflections) and the combinations of the symmetries that form a group. How many can you find?
It may help to think of the different patterns you can make with footprints including the walking pattern (glide reflection). Remember that, when you make a print from one revolution of the cylinder, you must not introduce translations.
This pattern involves a reflection $Y$ in a plane through the axis of the cylinder and a reflection $X$ in a plane perpendicular to the axis. The corresponding group must contain the combined transformation $XY$. Can you see that $XY$ and $YX$ both give a rotation about a line perpendicular to the axis of the cylinder? We shall call this rotation $R$. Further checking reveals that $X^2=Y^2=R^2=I$, $XR=RX=Y$ and $YR=RY=X$ so this frieze group is $\{I, X, Y, R\}$. Combining any number of the transformations $X$, $Y$ and $R$ in any order will always reduce to this group of four elements.
There are simpler groups $\{I, X\}$ and $\{I, R\}$ but as soon as we include two of the transformations $X$, $Y$ and $R$ we get all three transformations in the group. While there is only one group of the type $\{I,X\}$ there are many identical in structure (isomorphic) to $\{I, R\}$.
| Image
|
Image
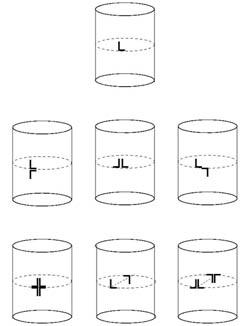
| We have now described five types of group depicted in the first five illustrations here which use a simpler motif than the footprint. The remaining groups involve glide reflections. The group shown in the sixth illustration is the group involving the identity and a glide reflection $G$ where $G^2=I$ so the group is $\{I, G\}$.This is the footprint pattern for someone walking on the beach.
We have already checked what happens when we form any combinations of $X$, $Y$ and $R$ with each other and discovered that they yield only five possible frieze group types.
It remains to check what happens when we combine $G$ with $X$, $Y$ or $R$ and to discover how many additional groups this gives.
First check $XG$. This gives a translation half way around the circumference of the cylinder so it is ruled out as one of the acceptable frieze group types because when printed it would give two translations with one revolution of the cylinder.
|
When we check $YG$ we find $YG=GY$ and the group is shown in the seventh illustration above. This combination also introduces a rotation about a line through the axis of the cylinder and perpendicular to the axis (the same type as $R$ shown in the fourth illustration). The seventh group is $\{I, Y, G, R\}$.
This discussion does not constitute a rigorous proof that there are only seven types of frieze group but when considering the cylinder it becomes intuitively obvious. A complete proof based on the symmetries of a cylinder, much simpler than the usual published proofs, can be given using 3 by 3 matrices in 3-space or using mappings in the complex plane.
In summary the seven frieze groups corresponding to the groups of symmetries of a cylinder with the transformations as defined above are :
(1) $\{I\}$ giving the frieze pattern ppppppppppp
(2) $\{I, X\}$ giving the frieze pattern EEEEEEEEE
(3) $\{I, Y\}$ giving the frieze pattern pqpqpqpqpqp
(4) $\{I, R\}$ giving the frieze pattern pdpdpdpdpdp
(5) $\{I, X, Y, R\}$ giving the frieze pattern HHHHHHHH
(6) $\{I, G\}$ giving the frieze pattern pbpbpbpbpbpbp
(7) $\{I, Y, G, R\}$giving the frieze pattern pqbdpqbdpqbd