The Derren Brown Coin Flipping Scam

Jungsun Choi and Junho Oh from Nanjing International School sent some wonderful thoughts to each part of this problem. In this solution I give each of their comments for comparison, along with some of my own thoughts and comments.

A key fact in this problem is that it takes, on average, 2046 flips to achieve 10 heads in a row. Analysis of this problem is fascinating because it draws together a fascinating mix of theoretical and numerical probability along with estimates and approximations.

 
1. Jungsun: There is an 1/2 chance to get a head of a coin each time. To get 10 heads in a row, an 1/2 chance has to be multiplied for 10 times. So, the formula to complete the coin scam on the first attempt is $(1/2)^{10}$. As a result, the chance of DB completing the coin scam on the first attempt is 1/1024.
 
Junho: The chance of DB completing the coin scam on the first attempt, which is to toss a coin and get 10 heads in a row, is very unlikely. When calculated, the probability of this happening is 1/1024 which is about 0.000967.
 

2. Jungsun: The chance to complete the coin scam on the first attempt is 1/1024, and it means that statistically, among 1024 trials (of 10 flips in a row), 1 trial may succeed to get 10 heads in a row.

Junho:  According to probability, there is a 1/1024 chance of getting 10 consecutive heads (in a run of 10 flips in a row). However, this does not mean that it will be exactly that number. It might take one person less throws to get 10 consecutive heads. Also, one might spend the whole day trying to get it, but not succeed.

Steve: The actual exact expectation calculation is complicated because DB did not do sequences of 10 coin flips: he carried on until 10 in a row were seen; this is not the same as doing several individual trials of 10 flips. The full computation involves conditional probability, and works out to be
 
$$
\begin{eqnarray}
E(10H)&=&E(10H|10H)P(10H)+E(10H|9HT)P(9HT)\cr
&+&E(10H|8HT)P(8HT)+\dots +E(10H|0HT)P(0HT)\cr
&=&2^{11}-2 = 2046
\end{eqnarray}
$$ 

The problem points to the fact that both the average and spread are relevant in probability calculations. I ran a simulation to determine the time of completion of trials in 2000 cases. You can view the data in this spreadsheet. The average for my trials was a little over 2053 (a little more because I terminated the trials at 10000 runs). The cumulative frequency chart was as follows:
 
 


3. Jungsun: Because his 5000 trials were all failed, he has to do the experiments again.

Junho: In order to make 10 consecutive heads, it is just a matter of chance. There is no exact number of flips that one can throw to get 10 consecutive coins; that is just a number of probability. There is no guarantee that x more flips will make 10 consecutive heads. Theoretically, one is supposed to get it after flipping 2046 times. But since this person did it already 5000 times and didn't get 10 consecutive heads, do it at least 2046 times again. (on average)
 
Steve: Coin flips are memoryless: regardless of how many previous flips have failed, I will still expect to have to make, on average, 2046 more flips. This is one of the most confusing aspects about probability to many people. Being able to think clearly 'What is the situation NOW? Do any PAST (i.e. happened) events effect any FUTURE (i.e. yet to happen) events?' really helps with probability.
 
 
4. Junho: If it takes 2046 flips to get 10 consecutive heads, theoretically, and a flip takes one second, that will take: 2046 seconds / 60 = about 34.1 minutes. But there are times when people get bored or get tired of flipping coins and since probability is never exact, it will probably take much longer than this. This is just the (average) amount of time it will take to get 10 consecutive heads.
 
Steve: Junho's points are very clear. To be reasonably confident of success we should probably allow more than the average of 2046 flips. As with any statistical computation we need to give a clear quantitative definition to any 'loose' terms. We could, for example, determine 'reasonable confidence' as equating to an '80% chance of success within a run of N flips'. Once this is done, we can compute. Given such large numbers, numerical simulations will serve us well when the exact computation is too difficult. Reading values off the cumulative frequency chart above shows that you would be 'reasonably confident' to succeed in less than 5000 flips.

5. Junho: This person can flip a coin in a second. There is only 10 minutes left which means this person can throw: $10\times 60 = 600$ throws. The possibility of getting 10 consecutive heads is 2046. If this person is lucky, he or she will get 10 consecutive heads, but is highly unlikely. The chances of achieving this is (about) $600/2046=0.293$.
 
Steve: In probability theory it is useful to distinguish between estimates for a probability and the exact probability. So, in this question we might reasonably estimate the chance of sucess as 600/2046 but would need to perform a computation or numerical simulation to determine the probability more precisely. This randomised spreadsheet shows that the chance is about 25%; alternatively we can read the value off the cumulative frequency chart above.
 

6. Jungsun:It is really helpful. Let's see the difference between $(50/100)^{10}=0.000977$ and $(55/100)^{10}=0.002533$: the probability of improved one is three times more than the previous one. As a result, it is really helpful to change the chance of heads on each throw.

Junho: Already, the head has a 5% more chance than getting the tail. This will save a lot of time and it will probably take less flips to get 10 consecutive flips, theoretically

Steve: These relatively small changes build up. With this biased coin, I found the following relative frequency chart and an average run time of 881 flips. 
 
 

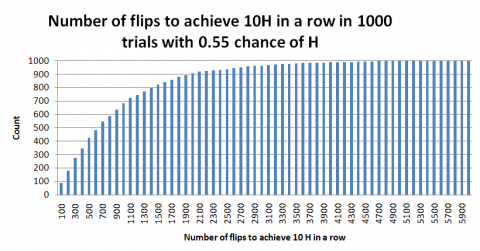
7. Jungsun: How high a coin goes up is one of the most important physical factor. If it is thrown too low, it is much easier to predict whether head or tail is going to be up. Also, the number of turns is also important. If a coin is thrown straight up, it can be controlled which side is going to be up.
 
Junho: Physical effects might bias the results or affect the outcome; any wind affecting the coin, the surface where the coin lands might be tilted
 
Steve: An old boss of mine used to be able to 'flip' a coin without it actually spinning; so beware! Slightly weighting one side of a coin can slightly alter its chance of landing up one face or the other. The previous part of this question shows that this might transpire to be significant.

8. Jungsun: He is quite unlucky, I believe. According to the time I expected, it only takes less than 3 hours. He, however, took 10 hours to complete and it is more than three times to the time that I predicted. I believed it only requires less than 1/8 of a day, but he spent more than 2/5 of a day which is quite unfortunate.

Junho: It took him 10 hours to get 10 heads consecutively. Theoretically, one is supposed to get it in 2046 flips. We do not know how fast he flipped the coins, but if we say that it took 1 flip took 1 second, he flipped: $10\times 60\times 60 = 36000$ times. He probably did fewer throws because he couldn't have thrown a coin in 1 second each time. We cannot determine whether he is unlucky or not because we do not have enough information to judge if he is unlucky or not. Also, what differentiates quite unlucky from very unlucky? We are not quite sure. If these vague points can be clarified, then we can come to a conclusion on how unlucky or lucky he was
 
Steve: As in earlier questions, we need to give precise quantitative definitions before we can perform a detailed analysis. Perhaps we might define 'very unlucky' as  'Imagine many people undertook the coin flipping experiment and recorded the time taken. Very unlucky people were in the longest 5% of times taken'. From the cumulative frequency chart, we define very unlucky people to take more than 6500 coin flips. If we can assume about 1 flip per 5 seconds then this equates to 7200 flips, which does indeed render Derrin Brown very unluckly with the amount of time taken.

9. Jungsun: The population of the UK is about 61,400,000. The chance of shortest number of flips is 1/1024. So multiplying  $61,400,000 \times  (1/1024)$ give $59960.9$. As a result, about $59961$ people are estimated to complete the coin scam in the shortest number of flips.
 
Junho: The shortest number of flips is of course 10. The chances of this situation happening is very, very low. But probability is just probability, it is just like the lottery. Britain has a big population, and if every single person tried this, it is to no surprise that someone might finish in just 10 flips. Others, might take days, weeks, and months to get 10 consecutive These people might not get 10 consecutive heads forever. As stated before, probability is just probability. It might never happen.
 
Steve: We are interested in estimating the length of the longest flip sequence. We can use our cumulative frequency chart above to help us estimate this: after about 1600 flips about half of the people flipping will have completed the process. Since the process is memoryless, about half of the remaining people will have completed the process after another 1600 flips. We need to halve 61 million about 25 times to get down to the last person. Thus, we estimate that the longest flip runs will be about $25\times 1600 = 40000$.

10. Jungsun: If there is no limit of time, unlimited number of heads in a row is possible. However, it would require heaps of, heaps of time :-)  

Junho: This stunt would be much more practical if the person stopped when there are 5 consecutive heads. This would not greatly reduce the failure rate but also increase the probability of actually achieving the wanted result.