Doughnut percents

This activity is designed to be tackled in pairs or small groups, but can also be completed individually. For more information on how this can be done in groups, take a look at the teachers' resources.

These printable domino cards can be put together to make four 'doughnuts' of four dominoes. The ends of dominoes which join together need to have equal value. 

For example, a doughnut could look like this:

Image

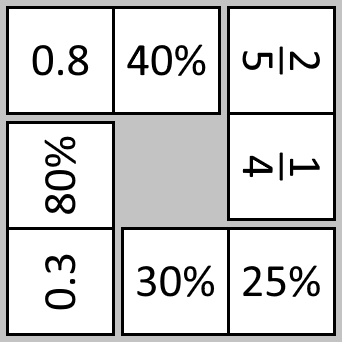
Have a go at making the four doughnuts. What do you notice?

Once you've made four doughnuts, you might like to try using the same set of cards to make two large doughnuts instead, with eight dominoes in each doughnut. 

Is it possible to make one very large doughnut, using all sixteen cards? And if it is possible, is there more than one way of doing this? How many can you find?

What we like to see

We have written an article on what we are looking for when we decide which solutions to publish.

You can share your work with us by typing into the form above or uploading a file.

What can I upload?

• Word documents
• PDF files
• Excel spreadsheets
• Images, including screenshots or photos of written work

If your work is on another app

You can also send us a link to your work on:

• Youtube/Vimeo
• Google Docs
• Sharepoint/Office 365
• Anywhere sensible on the internet!

Please make sure you have set the permissions so that we can access your work.

How we use your information

By uploading your solution here you are giving us permission to publish your work, either as a whole or edited extracts, on the NRICH website and in associated educational materials for students and teachers, at our discretion.

For our full terms of use regarding submitted solutions and user contributions please see https://nrich.maths.org/terms.

Your information (first name, school name etc) is optional. If supplied, it may be used for attribution purposes only if your work is published on the website. Data that you supply on this form (e.g. age if supplied, location if supplied) may also be anonymised and used for evaluation and reporting.

For more information about the University's policies and procedures on handling personal information, and your rights under data protection legislation, please see https://www.information-compliance.admin.cam.ac.uk/data-protection/general-data.