Encircling
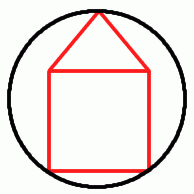
An equilateral triangle is sitting on top of a square.
What is the radius of the circle that circumscribes this shape?
Problem
The shape shown is of an equilateral triangle sitting on top of a square.
What is the radius of the circle that circumscribes this shape?
Image
Student Solutions
Congratulations James Page of Hethersett High School, Norwich on your solution to this question. Again there are many possible methods of showing that the radius of the circle is equal to the side of the square.
Image
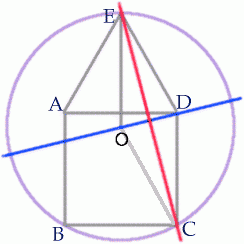
The blue line $OD$ is a diameter of the circle and a line of symmetry.
$\angle EDC = 150^{\circ}$ and $\triangle ECD$ isosceles so $\angle CED = \angle CDE =15^{\circ}$.
Now $\angle OED = 30^{\circ}$ so $\angle OEC = \angle OED - \angle CED = 15^{\circ}$ and hence the red line $EC$ is a line of symmetry for the quadrilateral $OEDC$ proving that the radius of the circle, $OC$ is equal in length to the side of the square.
