Of All the Areas
Can you find a general rule for finding the areas of equilateral triangles drawn on an isometric grid?
Problem
Of All the Areas printable sheet
You may wish to print off some isometric paper or use the isometric dotty grid environment for this problem.
This problem follows on from Isometric Areas and More Isometric Areas.
When working on an isometric grid, we can measure areas in terms of equilateral triangles instead of squares.
Here are some equilateral triangles.

If the area of the smallest triangle is 1 unit, what are the areas of the other triangles?
Can you see a relationship between the area and the length of the base of each triangle?
Will the pattern continue?
Can you explain why?
All the triangles in the first image had horizontal bases, but it is also possible to draw "tilted" equilateral triangles.

These triangles all have a "tilt" of 1.
Can you convince yourself that they are equilateral?
Can you find their areas?
Take a look at the hint for ideas on how to get started.
Can you find a rule to work out the area of any equilateral triangle with a "tilt" of 1?
Can you explain why your rule works?
What about areas of triangles with a "tilt" of 2?
What about areas of triangles with other "tilts"?
Getting Started
You may find it useful to take a look at More Isometric Areas.
These diagrams might help you to work out the areas of the tilted triangles.
The top diagrams show how drawing a non-tilted triangle around the tilted triangle could help you to find the area of the tilted triangle.
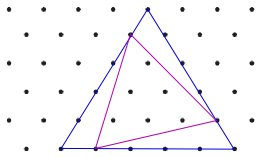

Area of tilted triangle = Area of blue triangle - Area of 3 green triangles
This diagram show some lines that can be drawn inside the tilted triangle:

Area of tilted triangle = Area of pink triangle + Area of 3 blue triangles
Student Solutions
Guruvignesh from Hymers College in the UK began looking at equilateral triangles with no tilt:
The triangle with isometric length 2 has an area 4, the triangle with isometric length 3 has an area of 9 and the triangle with an isometric length of 4 has an area of 16. Therefore, the area of the triangle is the square of the length of the base.
The pattern will comtinue because AF = SF$^2$ (area factor = scale factor squared), and so if we double the side to make another similar shape the area will be quadrupled and so will continue to be the square of the base.
Guruvignesh used a diagram similar to this one to explain why the tilted triangles are equilateral:

If the tilted triangle has a tilt of 1 then it has been rotated along the side of the equilateral triangle by 1 isometric dot. Since the inner triangle is equilateral, the lines labelled in green are also equal, and each of the 3 outer triangles has an angle of 60$^\text o$, we deduce that they are congruent using the side, angle, side rule.
This means that the lengths of the tilted triangle are all equal and that the red angles are all equal. Either of those facts tell us that the tilted triangle is equilateral.
Finding the areas of triangles with tilt 1
Guruvignesh used a similar diagram to find the areas of the triangles with tilt 1.

The area of the tilted triangle is the outer triangle take away the inner triangles, each of which is half a parallelogram. We know from Isometric Areas that the area of a parallelogram on isometric paper is double the product of the sides.
In the case of the smallest tilted triangle, the side length of the outside equilateral triangle is 3 so the green length is 2. So the area of the parallelogram is 2$\times$1$\times$2 = 4. Because each triangle has an area of 2, the whole area not taken uo by the tilted triangle is 6 and so the area is 9 $-$ 6, which is 3.
Now, we can find the area of all of the tilted triangles; the green triangle has an area of 7, the blue has an area of 13 and the red has an area of 21.
Matt from Swindon Academy in the UK used paralellograms inside the tilted triangles:

By splitting the triangles as shown and considering the halving ratio between triangles and parallelograms and rectangles (that the area of a triangle is half the area of a parallelogram, and we know how to find the area of a parallelogram on isometric paper from Isometric Areas), you can calculate the areas as $(1+1+1),$ $(1+2+2+2),$ $(4+3+3+3),$ $(9+4+4+4).$
The sequence $3,7,13,21,...$ can be solved:
First difference $4,6,8,$ second difference $2$.
$N^2:1,4,9,16$
$N^2+N:2,6,12,20$
$N^2+N+1:3,7,13,21$
Finding areas of triangles with other tilts
Matt went on to find the areas of equilateral triangles with tilt 2 and 3:

Using a similar method, solving the sequence of a tilt of 2 gives $N^2+2N+4$.

Using a similar method, solving the sequence for a tilt of 3 gives $N^2+3N+9$.
This allowed Matt and also Esther to spot a general rule. Matt said:
In general, the rules $N^2+N+1,$ $N^2+2N+4$ and $N^2+3N+9$ all fit the form of $N^2+AN+A^2$, where $A$ is the tilt of the triangle.
Teachers' Resources
Why do this problem?
In this problem, students are encouraged to measure areas using a triangular unit and come up with a general formula for finding the area of a tilted triangle. It brings together geometrical thinking, algebra, and sequences, and offers a different perspective on Pythagoras' Theorem.
Possible approach
For a similar problem using the more familiar context of a square dotty grid and leading to Pythagoras's Theorem, see Tilted Squares. For introductory work on using a triangular unit to measure area, see Isometric Areas and More Isometric Areas.
Allow time for reflection and discussion, drawing out ideas such as the use of non-standard units and the interesting result of square numbers.
Once a few areas have been found, encourage the students to make conjectures about the areas of much larger triangles with a tilt of 1, and to justify their ideas. The lesson could be structured in a similar way to the lesson in these videos of the task Tilted Squares.
Key Questions
Possible Support
You could start with the problems Isometric Areas and More Isometric Areas.
Focus on the justification that the tilted triangles are equilateral, and on calculating the areas rather than seeking generalisations.
Possible Extension
