Table Patterns Go Wild!
Nearly all of us have made table patterns on hundred squares, that is 10 by 10 grids. This problem looks at the patterns on differently sized square grids.
Problem
Table Patterns Go Wild! printable sheet
You might have made some times table patterns on hundred squares before. Some tables make vertical lines, some make diagonal lines and some make different patterns. Hundred squares are 10 by 10 grids, and in this problem we will call these '10 grids'.
Have a look at the 10 grids below.

Which times tables made these patterns? Why?
We are going to look at the patterns made on square grids of other sizes, from 4 grids (a 4 by 4 grid) to 9 grids.
These are patterns on a 7, a 5, an 8 and a 6 grid:

Which times tables made these patterns? Can you explain why they look like this?
Now it is time to do your own investigations. You can use grids drawn on squared paper or use this sheet of 10 grids.
Have a go at working out what makes vertical and diagonal lines on the different grids.
Can you make the checked pattern? What times table do you need to use on each grid?
Here are the top parts of some grids.
Can you identify which times table has been used to make each one?
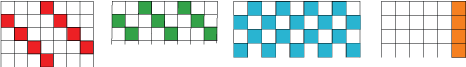
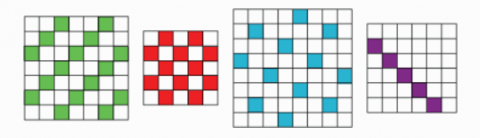
Here are some parts of various grids. This time we have not shown the edges of the grids.
Can you identify which times tables on which grids could have been used to make these patterns?

There may be more than one answer.
Getting Started
Try the various patterns out on squared paper.
Student Solutions
Well done to everybody who managed to work out which times tables were being shown in these pictures.
Dhruv from The Glasgow Academy in the UK investigated the different patterns that times tables make when they're drawn on the tens grids. This picture can be clicked on to make it bigger:

Good ideas, Dhruv! I wonder how these patterns would change if we changed the size of the grids?
We received a lot of solutions from the children at CHPS in Australia. Marley and Nina sent in the following picture explaining their ideas:

Well done for thinking so hard about this. I wonder if perhaps one of your checked grids doesn't quite work, as the gaps between shaded squares aren't always equal. I like your idea of using an odd by odd size grid to make the checked pattern with the two times table though!
The children from Chandlings School in the UK sent in these thoughts about the general patterns that different times tables on different grids will make:
Stephen: If you count the white squares until you reach the next shaded square (including counting that shaded square) that tells you the times table which has been shaded in.
Raffy: The reason the shaded times tables look the way they do is because of the amount of space left in a row to fit in the number that has been multiplied.
William: If the times table is one above or below the grid size the pattern will be diagonal. If the grid is one less than the times table the diagonal will go top left to bottom right corner. If the grid is one more than the times table it will go top right to bottom left.
Margaret: If the grid size is a multiple of the times table that has been coloured in, it will create vertical straight lines.
Theodore: If the grid is an even numbered size then even numbered times tables will go in columns and odd ones will go diagonally.
Richard: The two times table always makes a chequer pattern on an odd grid.
Mike: The four times table on a 10x10 grid makes a pattern where the shaded grids are always surrounded by white squares.
These are some good ideas. I particularly like the idea that we can say something about the relative sizes of the times table and the grid even when the only information we have is that the shaded lines are vertical, or that they're diagonal.
Shravani from Ganit Kreeda in Vicharvatika, India sent in this video explaining the solutions to some of the questions we asked in this activity:
Thank you for sending in this video, Shravani, it's really interesting to hear your explanations for each of these answers.
Shaunak from Ganit Manthan in Vicharvatika, India sent in the following solution to the grids we gave in this task:
Which times tables made these patterns? Why?
Here are the tables and why those patterns are made by that table:
The first one is made by the table of 5. This is the table because the table of any factor of 10 will form straight lines. Something interesting is that, if the table is 5, then the number of straight lines formed is 10 / 2 = 5. If the table is 2, then 10 / 2 = 5 lines will be formed. This will introduce a property for different grids: A factor of the grid number (if there is a 10 grid then the grid number is 10) will form a straight line.
The second one is made by the table of 9. This is the table because in the table of 9, the next box is + 10 - 1 spaces away, or in other terms, one box down and one box to the left. If you continue this pattern, then we see a diagonal line forming.
The third one is made by the table of 4. This is because the number of spaces between two boxes is 3, which means the next coloured box is after 4 spaces.
These are the tables mentioned above:

Which times tables made these patterns? Can you explain why they look like this?
The first one is made by the table of 3. This introduces another property: A factor of the number before the grid number will form a leftward diagonal line. 3 is a multiple of 7 - 1 = 6, so it forms such a pattern.
The second one is made by the table of 2. This introduces another property: If the grid number is odd, then a checked pattern is made by the table of 2. Here, the grid number is 5, so we get a checked pattern with the table of 2.
The third one is made by the table of 5. This is because the difference between two coloured boxes is 4, which means the next coloured box is after 5 boxes.
The fourth one is made by the table of 7. This introduces another property: The number before the grid number will form a rightward diagonal line. 7 is 6 + 1, so it forms such a pattern.
These are the tables mentioned above:
Have a go at working out what makes vertical and diagonal lines on the different grids.
Using some of the properties stated above, I was able to make straight lines and diagonal lines with any grid.
Can you make the checked pattern? What times table do you need to use on each grid?
Due to a property stated above (If the grid number is odd, then a checked pattern is made by the table of 2), I can make a checked pattern only if the grid number is odd.
Here are the top parts of some grids. Can you identify which times table has been used to make each one?
The first one is made by the table of 4.
The second one is made by the table of 3.
The third one is made by the table of 2.
The fourth one is made by the table of 6.
These are the tables mentioned above:

Here are some parts of various grids. This time we have not shown the edges of the grids. Can you identify which times tables on which grids could have been used to make these patterns?
The first pattern can be made by any grid between 6-12 grid and the table is one greater than the grid number.
The second pattern can be made by any grid between 5-12 grid, and the table is one less than the grid number.
The third pattern is made by the table of 6 in 9 grid.
The fourth pattern can be made by 8 grid and 11 grid and the table is always 3.
The fifth pattern can be made by 9 grid and 11 grid and the table is, in both cases, 2.
These are the tables mentioned above:

These are some excellent ideas, Shaunak, and you've explained all of this really clearly. The only thing I disagree with is that I think the purple shaded grid (at the very left of the final picture) can't represent the six times table, because there is a gap of at least six between each pair of numbers.
We also received similar solutions from: Bella and Theo from Twyford School in the UK; Aleiyah, Evangeline, Amelia, Kai, Elijah and Sentwali from William Konkin Elementary School in Canada; Luna from CHPS; Lucas and Teddy from Over Primary School; and Abhyudh, Viyaan, Aditi, Mridula, Pushan, Veyhant, Anika, Kiaan and Shreehari from Ganit Kreeda, Vicharvatika, India. Thank you all for sharing your ideas with us.
Teachers' Resources
Why do this problem?
It can also add to their ideas of pattern and design.
Possible approach
If learners have not done many table patterns on hundred squares you could start by doing some of these. It is important that they do not see these as a series of straight lines, so it is advisable to get them to do the three times and four times tables before they embark on the two and five times. They should be asked why the tables of twos and fives make straight lines. Of course the word "factor" might pop up here and there.
There are two photocopiable "problem sheets" for learners to identify the tables and grids. These have more on them than the ones given in the problem. This sheet (A) has clearly defined grids and so is much easier than this one (B) which is a real challenge. In sheet B the sizes of the grids are more ambiguous and which may, therefore, have more than one answer. Squared paper is useful in investigating these.
At the end of the lesson learners should be asked to say what makes the different patterns. The factors of the grid number should be discussed and also the idea of one more than and one less than. It is possible here to introduce or practise using a letter to stand for "any number".
You could also discuss what makes an interesting all-over pattern.
Key questions
Possible extension
Those who are really confident with the grids up to ten could predict what they will get and then explore eleven and twelve grids (which can be drawn on squared paper). They could also be expected to express their findings in algebraic terms where possible.
Learners could investigate recording more than one multiple on a grid, in the same colour.
What happens if the grid is different? Alan Parr suggests challenging learners to explore table patterns on a 'snakes and ladders' board, for example. You can read about some examples in his blog post.
Possible support
Suggest concentrating on the patterns on hundred squares and $10$ grids.
