Children's mathematical graphics: understanding the key concept

Introduction

The key concept in understanding and supporting young children's mathematical graphics is knowing the difference between children 'recording' a piece of mathematics after they have done it practically, as opposed to children representing their own mathematical thinking (i.e. children's mathematical graphics).

Children's mathematical graphics is a term we originated to refer to the visual marks and representations (graphics) young children choose to use to explore mathematical meanings and communicate their thinking. It includes a wide range of graphics such as scribble-marks, drawings, writing, invented and standard symbols. In education 'mark-making' is often used as a generic term for children's early explorations such as drawing or writing and there is confusion about its use and application. When discussing specific aspects such as 'drawing', 'writing' or 'children's mathematical graphics', it is preferable to use these terms.

Ofsted repeatedly raises concerns regarding children's over-reliance on formal written methods, emphasising the importance of children's informal methods of notation. Annual inspection reports highlight the importance of building links between children's mental and written methods and for greater opportunities for children to use and apply mathematics.

Ginsberg first identified written mathematics as the aspect that young children find most difficult (1977). Later Hughes demonstrated how young children could represent quantities they had counted by using their own, self-chosen representations (1986). Our research has explored this important aspect in depth, charting children's understanding of the written language of mathematics from birth to eight years (e.g. Carruthers & Worthington, 2005, 2006; DCSF, 2008, 2009). The 'Williams Maths Review' features our work on children's mathematical graphics, making specific recommendations about its role in supporting abstract mathematical symbolism (DCSF, 2008: 4 / 34-37).

Recording mathematics

Historically the emphasis has been on children 'doing' mathematics, working something out with practical resources and then 'recording' it afterwards. However our research has shown that this has limited value. Recording places the emphasis on marks, symbols and drawings as a product, and is a lower level of cognitive demand. The National Numeracy Strategy emphasised that children do not need to record their mathematics if they can work something out mentally, neither do they need to record something they have already worked out in a practical context with resources (QCA, 1999).

Exploring differences between 'recording mathematics' and 'representing mathematical thinking' at the MA's 2009 conference in Cambridge, led to rich discussion and raised considerable interest.

Representing mathematical thinking

To differentiate between the early written mathematics that most young children experience and children's mathematical graphics, we use the term 'representing': children represent their internal, mental representations, in effect - exploring their mental methods on paper. Children's own graphics support deepened thinking about the mathematics in which they are engaged, and significantly, about their use of symbols and other visual representations to signify meanings. They enable children to build on what they already know and understand - not as a pre-cursor to abstract written symbolism of mathematics but as a meaningful and continuing process throughout the Foundation Stage and Key Stage 1.

Image	Image
Figure 1: "A cross means you lose."	Figure 2: "This is where you double-lose."

Mathematical disconnections

Image

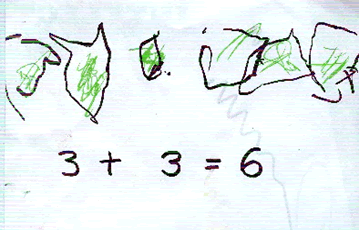
Figure 3: Recording - Leo (aged 4 years 6 months)

Figure 3 shows an example of a child's 'recording'. Leo's teacher showed the children addition using multilink. Giving each child three cubes to count and then three additional cubes, she asked the child how many cubes they had altogether. Leo counted from the first group "$1, 2, 3$" and then continued counting the cubes in the second group, "$4, 5, 6$". His teacher wrote the calculation on the white board commenting "$3$ add $3$ equals $6$". She asked the children to draw how many cubes they had altogether. Some of the children copied what the teacher had written: Leo hesitated so his teacher wrote "$3 + 3 = 6$" beneath the cubes Leo had drawn.

The children's drawings were all virtually the same: the only differences were the ways the children had drawn and coloured the cubes. In effect the teacher had done all of Leo's thinking for him - preventing him exploring possible ways that might make sense to him. An unintended consequence of working in this way leads to children's confusion about written calculations and superficial understanding of the abstract written language of mathematics.

Mathematical connections

Image

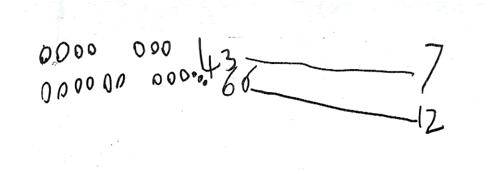
Figure 4: Children's mathematical graphics (representing personal mathematical thinking) - Jack (4 years 8 months)

Figure 4 shows an example of addition in another reception class where children were encouraged to represent their own mathematical thinking using their mathematical graphics.

Jack's teacher put a plate of grapes on the table where his group was sitting, adding some blank paper for any of the children who might want to explore their ideas on paper. She invited the children to choose a small quantity of grapes to put in each of two small dishes and work out how many grapes they had altogether. Jack chose to use paper and first drew two separate sets of grapes, leaving a gap that allowed his first calculation to be read as '$4$ and $3$' (we term this an 'implicit symbol'). He confirmed the quantities by writing the numerals and drew a line between these and the final '$7$', using the line to signify an equals sign.

Since Jack represented his mathematical thinking in ways he chose, his calculations were personally meaningful. Two of the children worked out their calculations mentally, whilst others chose to explore their ideas on paper, connecting mental and written methods. They used a range of personal graphics including words, numerals, drawings and invented mathematical symbols. Significantly children's mathematical graphics support children's processes ('using and applying mathematics'; DfES, 2006). The important point is that the children were making their own connections, building on their early understanding of marks and symbols and using them to make mathematical meanings.

Image

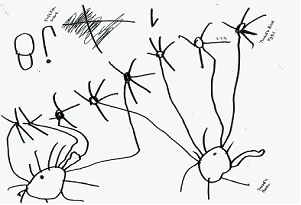
Figure 5: "Can $8$ be shared equally between two?" Using his own mathematical graphics, Kamrin solved the problem by inventing 'Tweedle Birds' and sharing eight eggs equally between them.

Key attributes of children's mathematical graphics include:

• children's own choice to represent their mathematical thinking
• children's own meanings - both independent and co-constructed (rather than copied)
• children's own graphics (drawings, writing, symbols, marks)
• children's own layouts
• children challenge themselves as they explore their mathematical thinking and meanings, communicate their ideas and solve problems

Some aspects of the adult's role:

• Adults value children's mathematical graphics
• Observing children closely allows adults to understand more about individual's thinking
• Annotating children's mathematical graphics allows adults to sensitively uncover children's thinking and meanings

Conclusion

• A culture with a significant focus on mathematical mark-making in line with early writing, through, for example, role-play and the use of popular mathematical signage in the environment
• A learning environment that encourages children to choose to use their own mathematical graphics to support their mathematical thinking and processes' (p. 37)

Some principles of children's mathematical graphics

• Young children continually explore and make meanings in their play
• They sometimes choose to use their own mathematical graphics to explore, make and communicate mathematical meanings
• They represent their mathematical thinking in their own ways
• They build on what they already know about the meaning-potential of marks and visual representations to also carry mathematical meanings
• They co-construct understanding about mathematical notation through collaborative dialogue
• They focus on processes of learning, rather than notation as a product.

References