Farhan's poor square
Problem
From the measurements and the clue given find the area of the square that is not covered by the triangle and the circle. Give your answer as a formula and then calculate the area correct to two decimal places. (This problem was created by Syed from Foxford School and Community College).
Student Solutions

Splendid solutions to Farhan's problem came in from Shabbir Telani, age 13, Jack Hunt School, Peterborough, Prav Idaikkadar,age 13, and Megan Mitchell, age 14, North London Collegiate School Maths Club, Richard Mason, Madras College, and Rachel Evans, the Mount School York. This is Shabbir's solution:
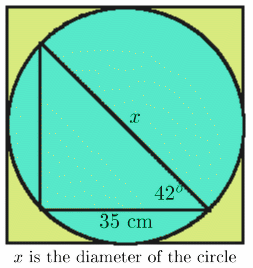
Using trigonometry:
$$ x = \frac{35}{\cos 42^o} = 47.09714 = 47.10$$ (to 2 decimal places).
To find the area of the square not covered by the circle work out the area of the square minus the area of the circle.The formula for the area is
$A = x^2 - \pi \left(\frac{x}{2}\right)^2$
So the area of the square not covered by the circle and triangle is 2218.14 - 1742.12 = 476.02 cm 2 (to 2 decimal places).