Inclusion Exclusion

How many integers between 1 and 1200 are NOT multiples of any of the numbers 2, 3 or 5?

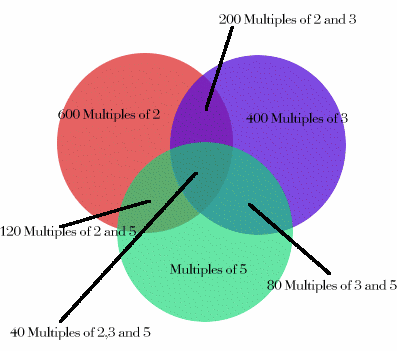
Working along the same lines, Emma and Laura from The Mount School, York sent the diagramand Lorn from Stamford School sent the solution below:

Simplify the problem by trying 1-30 (because 2 x 3 x 5 = 30 and 30 is a factor of 1200).

First I crossed off all the multiples of 2 (even numbers). Then I crossed off all multiples of 3, then all multiples of 5. I then counted 8 numbers which were not crossed off.

I tried 31-60 and found a pattern.
Comparing 31-60 and 1-30, the crossed off numbers corresponded.
This is not surprising since you get the numbers in the second set just by adding 30 to the numbers in the first set.
I also noticed that the numbers I did not cross off were prime numbers and 2, 3 and 5 are prime.

There are 40 sets of 30 numbers from 1 to 1200 (1-30, 31-60, 61-90 ... ).
From this I conclude that in each set there are 8 numbers that are not multiples of 2, 3 or 5, so there are 8 x 40 = 320 numbers altogether that are not multiples of 2, 3 or 5.

Lorn found another method, using similar ideas, sparked from the Venn diagram shown in the original question:

The diagram shows three sets of numbers: multiples of 2, multiples of 3 and multiples of 5.
When counting all the numbers in the three sets (600 + 400 + 240 = 1240) some numbers are counted twice and some numbers are counted 3 times.
Deducting the number of 'double counted' numbers we get 1240 - 200 - 80 - 120 = 840. Now the 'triple counted' numbers have been removed 3 times so we need to add on 40 to include them, giving 880 numbers which are multiples of one or more of the given numbers.
It follows that 1200 - 880 = 320 numbers are not multiples of any of these numbers.

Venn diagram showing whole numbers from 1 to 1200

Congratulations for your work on this problem to Samantha of Hethersett High School, Norfolk, Jenny, Caroline, Emma, Rachel and Beth from the Mount School, York and to Ben.