Human Food
Problem

Sam stacks cans in his shop in triangular stacks, one can deep, (see the problem Cat Food ).
Jennifer from the Mount School York warned Sam that stacks of cans like this are very likely to fall over. It's better to stack in a pyramid: for example. $P_4$ has $16$ on the base, then $9$ then $4$ and finally $1$.

In his shop Sam has a display of cans of baked beans in three triangular stacks.
He decides to rearrange the display and realises that he could either make a single large triangular stack with the same number of cans or stack them all in a square-based pyramid.
How many cans has he got and how was his first display arranged?
The following problem was invented by Kerry of Lasswade High School:
Sams gets deliveries of $45$ cans every Monday and Wednesday.
He received his Monday delivery and used all the cans to make three triangular stacks.
On Tuesday he had three customers all of whom bought $12$ cans each.
After his Wednesday delivery he found that with all his leftovers from Monday and his new cans, he could make three triangular stacks in more than one way.
How many ways could he make three triangular stacks?
What are the ways?
Student Solutions
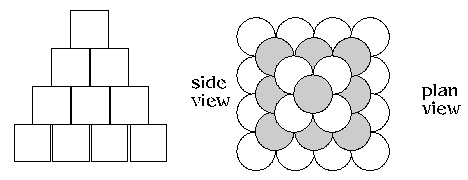
Scott Lewington, age 11, Lea Manor High School and Ling Xiang Ning, Allan, age 12, Raffles Institution, Singapore solved the Human Food problem.
They found square based pyramids with the same number of cans as one triangular stack with a depth of one can (a triangular number of cans) and then three triangular stacks to make up of the same number of cans altogether.
The triangular numbers are: 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105,...
The square based pyramid numbers are: 1, 5, 14, 30, 55, 91, 140, 208,...
As we can see, there are two numbers that appear in both lists, 55 and 91. This means that both of them are possible to be a square pyramid (with a 5 by 5 base or a 6 by 6 base) and a triangular stack (with a base of 10 or of 13). Now, we just have to find the three triangular stacks 55 and 91 cans can be made into.
For 55 cans, it could be made into triangular stacks of 6, 21 and 28 (T 3 + T 6 + T 7 ).
For 91 cans, it could be made into triangular stacks of 10, 15 and 66 (T 4 + T 5 + T 11 ) or of 3, 10 and 78 (T 2 + T 4 + T 12 ) or of 15, 21 and 55 (T 5 + T 6 + T 10 ) or 10, 36 and 45 (T 4 +T 8 + T 9 ).
There are other possible solutions. This type of investigation can best be pursued using a spreadsheet with formulae for the different types of patterned numbers in different columns. This leads to conjectures about the algebraic relationships between different patterned numbers which may be proved algebraically.
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension


