Ramping It Up
Problem
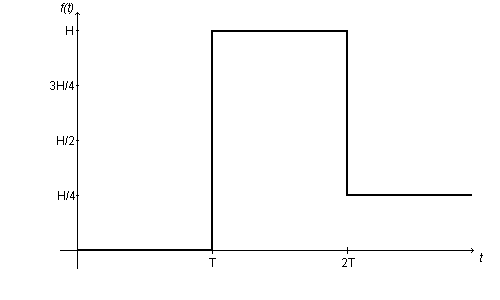
At a time T, a car mounts a curb of height $H$, and its front suspension undergoes a sudden change. At a time 2T, the car drops down the other side of the curb to $\frac{1}{4}H$. It is suggested that the graph of this process is as given as a function $f(t)$ above.
Try to work out the graph of $f $ '$(t)$ against $t$. What parts make sense and what parts don't? Could you alter the graph of $f(t)$ slightly to make the derivative function make more sense?
Next imagine that a car drives at a steady $20$ km h$^{-1}$ over a concrete block of height $10$cm and rectangular cross section of width $50$ cm. Make a mathematical model of the height of the front suspension over time. Be clear as to your assumptions and make a clear note of any possible refinements to your model.
What does your model say about the derivative of the height over time?
What is the maximum G-force the suspension of a car is likely to be subjected to in normal use?
On a physical note, think about the implications that this sort of modelling process might have on the design of shock-absorbers for cars.
Getting Started
You could consider replacing the vertical lines by very steep gradient lines.
To relate the problem to acceleration, recall that the acceleration is the second derivative of the position.
Don't forget that you are not allowed to have 'infinite' values on a graph.
This problem introduces the mathematics behind 'step functions' and 'Dirac delta' functions.
Student Solutions
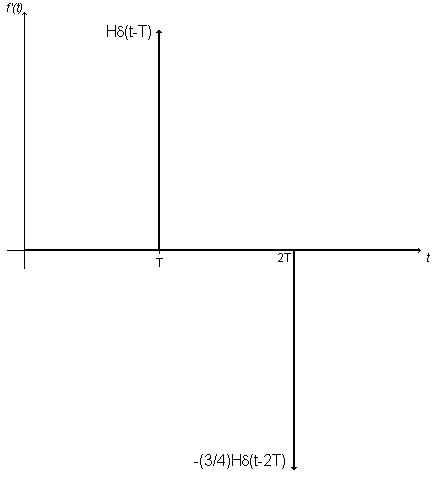
The gradient is infinitely steep at the points where there is a step in value. These arrows are called delta functions. They are thought of as infinitely high and thin, and have a notional area equal to the value of the step jump. Thus when you integrate this derivative, you get back to the original step function.
A system's (for example a car suspension) response to an impulse (you might think of it as a sudden "bang") is very useful, and can be used on a process called "convolution" to find a system's response to any input.
