What is the question?
These pictures and answers leave the viewer with the problem "What
is the Question". Can you give the question and how the answer
follows?
Problem
Image

|
The answer is 49.
What is the question?
Why does it work?
|
Image

|
The answer is 42.
What is the question?
Why does it work?
|
Image

|
The answer is 63.
What is the question?
Why does it work?
|
Image

|
The answer is 56.
What is the question?
Why does it work?
|
Does this always work?
Can you extend the method to other numbers?
Getting Started
Image

|
The answer is 49.
What is the question?
Why does it work?
|
Image

|
The answer is 42.
What is the question?
Why does it work?
|
Image
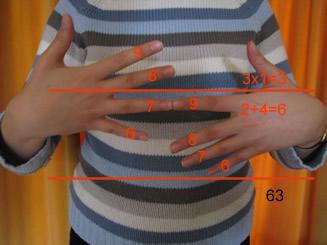
|
The answer is 63.
What is the question?
Why does it work?
|
Image

|
The answer is 56.
What is the question?
Why does it work?
|
Teachers' Resources
Why do this problem
This problem is based on one of many ways of supporting multiplication. The examples consider numbers from 6 to 9 but does the method work, or can it be modified to work for other numbers? The focus is on the why, rather than any sense that this is a preferable way of calculation. But this is an interesting representation nevertheless and leads to the question, "What sort of person could have thought of this for the first time?".
Possible approach
Rather than show the images on the site it might be good to take a small number of learners in the group into your confidence and ask them to show examples and give the answers without explanation, asking the rest of the group to make sense of the code.Once the code has been cracked the question has to be asked why it works. This may be something you wish to leave learners to think about over time, returning to the problem if and when any light is shed.
Key questions
Can you find a way of defining the number of fingers you multiply and the numbers you add?Possible support
Discussion of complements of 10 first might support learners in making the necessary connections.Possible extension
Could you start at 16 on each hand? What adjustments would you need to make?How about 26, 36 etc?
Could you use 11 to 15?
