LCM Sudoku II
You are given the Lowest Common Multiples of sets of digits. Find the digits and then solve the Sudoku.
Problem
By Henry Kwok
Image
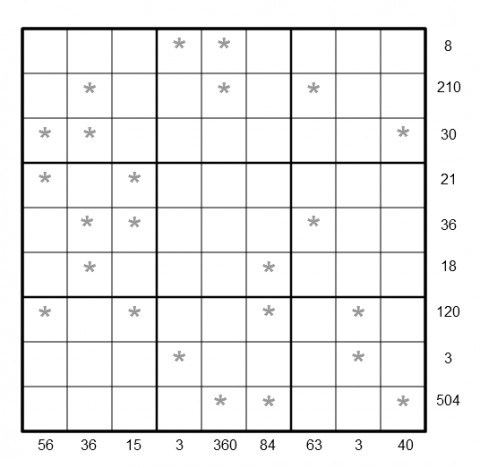
Rules of LCM Sudoku
Like the standard sudoku, this sudoku variant has the basic rule:
- Every row, every column and every $3\times 3$ box in the grids contains the digits $1$ through $9$.
The puzzle can be solved by finding the values of the unknown digits (all indicated by asterisks) in the squares of the $9\times 9$ grid. At the bottom and right side of the $9\times 9$ grid are numbers, each of which is the Least Common Multiple (LCM) of a column or row of unknown digits marked by asterisks.
Altogether $18$ Least Common Multiples of $9$ columns and $9$ rows of unknown digits are given as clues for solving the puzzle.
As an example, the LCM of $3$, $9$, $6$, $4$, $2$ and $1$ is $36$. In the puzzle, the LCM of the four unknown digits in the second column beginning from the left of the $9\times 9$ grid is $36$, while the LCM of the four unknown digits in the seventh row beginning from the top of the $9\times 9$ grid is $120$.
After finding the values of all the unknown digits, the puzzle is solved by the usual sudoku technique and strategy.
Getting Started
Caitlin kept a record of the order in which she filled the Sudoku.
She filled the cell marked 1 first, then the cell marked 2, then the cell marked 3...
You might like to retrace her route to fill in the cells in the same order, though this is just one possible route through the problem.
You can print her journey here.
Student Solutions
Image

