Galley Division
Can you explain how Galley Division works?
Age
14 to 16
Challenge level
Problem
The 'Galley' method of division was probably the most widely used method of division prior to the 1600s. It is called 'Galley' because, when completed, a division looks a bit like a galley (boat).
The Galley method is thought to be Hindu in origin and an early version of this method was known to be used in the ninth century by a Persian called Al-Khowarizmi. It is still taught in parts of North Africa and the Middle East today.
This is how you could work out $65284$ divided by $594$ using the Galley method:
Image
Can you see the two numbers I started with?
The calculation tells me that $ 65284 \div 594 = 109$ remainder $538$.
Can you see the answer and the remainder?
Here's another division done using the Galley method:
Image
What division do you think is being done here?
What is the answer to this division?
Here are two video clips of divisions using Galley arithmetic:
If you are struggling to see what is happening, try the division using your own method and see if you can recognise numbers that are appearing in the galley method that are also in your own recording. If you need further guidance, there is a division, showing each of the main steps and some explanation, in the hints section of this problem.
Can you work out the answers to the following divisions using the same method? $$2986 \div 47$$
$$76254 \div 235$$
Why does the method work?
How does this method compare with our modern methods of division?
Getting Started
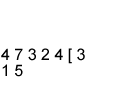
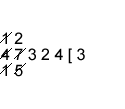
$47324 \div 15 = 3154$ rem $14$
Student Solutions
In Nyeong Chang sent us the solution to the two divisions set in the problem, set out using Galley Division, and explained a little about how it works:
Image
Not only are the answers same as when the long division method was applied, but the same numbers are appearing. This works because the basic mechanism of division is the same. What is done in both long division and Galley division is seeing how many of the divisor can fit into the dividend one digit at a time, and then calculating the remaining number, and repeating until a remainder smaller than the divisor is left.
Mao Yamamoto worked out $76254 \div 35$ rather than $235$ but showed very nicely how the standard long division method relates to the Galley Division method by setting out the Galley Division in the same way:
The method works in the same way as our modern methods of division. The only difference is that when the denominator is more than one digit and subtraction is needed, denominators are separated as one digit and calculated. For example, in the calculation $76254 \div 35$ below, in the modern method we need to multiply $35$ by $2$ and subtract from $76$. In Galley division, we multiply $3$ by $2$ and subtract from $7$. Then we multiply $5$ by $2$ and subtract from $16$.
Image
Compared with the modern methods of division, this Galley Division may be easier for some students as it allows them to subtract numbers with fewer digits.
Teachers' Resources
Why do this problem :
This problem draws attention to the way digits are arranged in a written calculation. The traditional representation for basic computation can be taken for granted. This problem allows the display choices made to become conspicuous and appreciated.
Possible approach :
Ask the group to do the first calculation on a calculator to get 'an answer' and then ask questions about what that decimal display means.
Draw attention to the fact that people have been successfully calculating results of value for centuries, long before electronic calculation, and ask what calculations might have been important and why.
Ask how these calculations might have been achieved and in particular why some of our standard non-calculator algorithms work (include long multiplication, and long division, plus finding prime factors if that is within the students' experience).
Draw the students into a similar discussion about the Galley method for arranging and holding digits during a calculation.
Ideally this should be group work with lots of talk : noticing possible positioning of digits, reasoning to support or challenge the validity of those conjectures, and gradually building up a complete understanding of the whole method. This can then be practised with new numbers, rehearsing the reasoning in the process.
Key questions :
- What does 'division' mean ?
- How would you work out 65284 divided by 594 ?
- Without a calculator ?
- How do we know that's an 'OK method' ?
- Any thoughts on how the Galley way of setting out the calculation works ?
Possible extension :
Composite NotionsUnusual Long Division - Square Roots Before Calculators