Crossed Ends
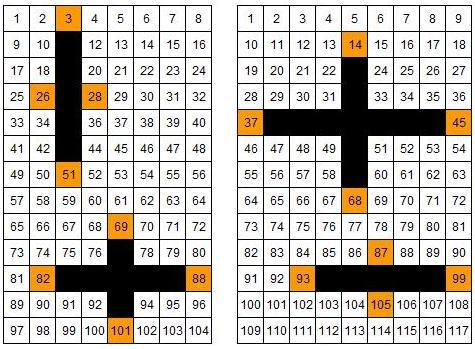
Crosses can be drawn on number grids of various sizes. What do you notice when you add opposite ends?
Problem
Crossed Ends printable worksheet
These crosses can be drawn on number grids of various sizes.
Add opposite pairs of orange numbers
(i.e. north + south, east + west).
Notice anything?
Try a few more.
Now try adding opposite pairs on crosses with just two lines of symmetry, like these:
What do you notice?
Can you explain your findings?
Experiment with grids of various sizes.
You may find these printable sheets useful:
Number Grids - width 3, 4, 5 and 6
What happens if you add the orange squares in adjacent pairs? (try N + W, S + E )
Can you predict in advance how the totals will relate to each other?
What does it depend on?
Is it the same if you added them the other way round? (i.e. N + E, S + W)
Can you explain your findings?
Getting Started
Try drawing some of the crosses on a 1-100 square (a size 10 grid). The patterns may become more apparent.
Consider using algebra to represent the relationships between the different end cells.
Student Solutions
Mohit, Harry, Jimbob, Sanjay,Imo and Jazzy all found that
When you add one pair of opposite numbers it is always equal to the other pair.
i.e. If you add N+S, W+E you get the same answer, and that answer is twice the number in the middle of the cross, whatever the size of the cross and the grid.
If you add N+S+E+W you always get 4x middle number.
Kang from The Garden International School sent us a clear solution to the problem:
Adding opposite pairs on a cross:
Always, the result will be the same with each pair.
Using algebra, it will be easy to explain and understand.
In a cross, the pairs are (up + down) & (left + right).
If the middle square is x, right will be x+1 and left will be x-1.
On a size 10 grid, up is x-10 and down is x+10.
They all add up to 2x.
The explanation for a bigger cross is the same, but with bigger numbers of + and - (assuming always the opposite sides of the cross are of equal length).
Adding adjacent pairs on a cross:
It is the same, but there is a difference and it is always the same.
If it is added together such as (N+E) & (S+W),
N = x-10
E = x+1
S = x+10
W = x-1
(x-10) + (x+1) = 2x-9
(x+10) + (x-1) = 2x+9
The difference between the adjacent pairs = (2x+9) - (2x-9) = 18
For other pair of adjacent sides, it works in the same way.
Harry from Brewood Middle School explained it differently:
Teachers' Resources
Why do this problem?
This problem offers an interesting context in which to introduce and develop students' understanding of algebraic notation.
Possible approach
This printable worksheet may be useful: CrossedEnds.pdf
Display a number grid and select a 'square cross'. Ask one side of the class to add the top and bottom numbers, and the other side to add the far left and far right numbers. "Surprised?" Repeat with a 'square cross' of a different size.
Hand out some number grids and ask students to check what happens with other square crosses. As students become convinced that the totals will always be equal, suggest they move on to 'rectangular crosses'.
"It's not enough to know what happens, we need to understand why it happens". Ask students to work in pairs and challenge them to come up with a really clear explanation of why the totals always match.
Bring the class together to compare explanations.
If it is not suggested, select a grid and introduce the idea of labelling the top cell $x$ and ask how the other three cells at the end of the cross could be labelled. Then add the expressions in the opposite cells. As often as possible, ask students to relate specific expressions to the numerical context, "What does it mean here? Would it still be true over here?"
Ask for a volunteer to demonstrate how the technique would work on a different grid or cross shape. Do the two totals still match? Ask for a volunteer to fill in the ends of a cross when you put x in a different end cell. "What does this mean? Do you think it matters where we place the x?"
Set students to work in pairs, placing $x$ in various different cells and confirming that the proof that the totals are equal always holds true. They could try other cross shapes or grid sizes if they have time. Placing x at the centre of the cross can help students appreciate why the opposite cells will always add to the same total.
Move on to comparing N+W with S+E.
Suggest that they begin algebraically, and just look at numerical cases to check that they do what they expect. Ask someone to select a grid, a cross, and the position of $x$. Ask students to then supply and justify the expressions for all the end cells.
"How do the totals compare?" (expect comments like not equal, a fixed difference). Ask students to pick their own cross of the same size and on the same grid, and confirm that the algebraic predictions are correct. Ask students to repeat this process for their choices of grid, cross and position of $x$.
Key questions
How are the numbers on the grid related to each other?
How can I represent this algebraically?
Possible extension
If I have a cross and tell you what (S+E)-(N+W) comes to, can you work out what my cross looks like?
Some students may like to generalise across the grid sizes.
Does anything interesting happen with the products of the ends of the crosses?
Possible support
This problem may be more accessible when applied to a 1-100 square (a size 10 grid) in which the relationships between the end points may be clearer to see.
An easier problem, also using 100 squares and place value like this is Diagonal Sums
