Dilution Series Calculator
Which dilutions can you make using 10ml pipettes and 100ml measuring cylinders?
Problem
This interactive diagram shows a dilution series made from four dilutions of an initial bacterial solution. At each stage of the dilution, a quantity of the culture is diluted with a quantity of the medium

Other problems
Getting Started
Don't be put off by the four stages. To begin with, how would you set up the numbers to mimic a single dilution?
Student Solutions
A solution to an interactive of this sort is best done with a worked example:
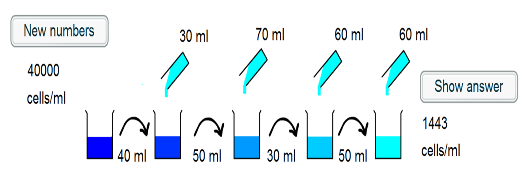
1) The intial beaker contains 40000 cells/ml. 40ml of this is taken, and so there are $40000 \times 40 = 1.6 \times 10^6$ cells placed into the second beaker.
2) 30ml of water is added to the second beaker, such that the cells are in a volume of 70ml. The concentration is now $\frac{1.6 \times 10^6}{70} =2.29 \times 10^4$ cells/ml.
3) 50ml of this suspension is taken and placed into the third beaker, and so $2.29 \times 10^4 \times 50 = 1.14 \times 10^6$ cells are transferred.
4) A further 70ml of water is added, such that the cells are in a 120ml suspension. This corresponds to a concentration of $\frac{1.14 \times 10^6}{120} = 9.52 \times 10^3$ cells/ml.
5) 30ml of the suspension is transferred, which corresponds to $30 \times 9.52 \times 10^3 = 2.86 \times 10^5$ cells.
6) 60ml is added to the fourth beaker, and so the cells are in a 90ml volume. The concentration is hence $\frac {2.86 \times 10^5}{90} = 3175$ cells/ml.
7)50ml of the suspension is transferred to the final beaker, corresponding to $ 50 \times 3175 = 1.59 \times 10^5$ cells
8) 60ml more water is added to give a final volume of 110ml. Thus the final concentration is $\frac{1.59 \times 10^5}{110} = 1443$ cells/ml
Of additional interest is a general rule.
$n_f$ is the final cell concentration
$n_i$ is the initial cell concentration
$V_1, V_2, V_3, V_4$ are the volumes transferred to the second, third, fourth and fifth beakers respectively
$V_a, V_b, V_c, V_d$ are the volumes added to the second, third, fourth and fifth beakers respectively.
Thus,
$$n_f = \left(\frac{\left(\frac{\left(\frac{\left(\frac{n_i \times V_1}{V_1 +V_a}\right) \times V_2}{V_2 + V_b}\right) \times V_3}{V_3 + V_c}\right)\times V_4}{V_4 + V_d}\right)$$
$$ = \frac{n_iV_1V_2V_3V_4}{(V_1 + V_a)(V_2 + V_b)(V_3 + V_c)(V_4 + V_d)}$$
Thus, the dilution series calculation reduces to multiplication of fractions.
Teachers' Resources
Why do this problem?
This activity gives repeated practice in the proportional reasoning required to understand dilution calculations. It is surprising how even quite skilled mathematicians find this quite tricky. Clear thinking is required and this will be developed by the problem.
Possible approach
Key questions
Possible extension
Possible support
