The Not-so-simple Pendulum 1
See how the motion of the simple pendulum is not-so-simple after all.
Problem
A simple pendulum is a heavy weight, or bob, swinging from the end of a inextensible string. However, the maths required to model this properly is far from simple! In this question we see how the ideas might build up in complexity.
The bob of mass $M$ on an inextensible string of length $L$ is pulled to a displaced angle of $\theta$ from the vertical. Draw a diagram and work out the tangential force on the bob in terms of $\theta$.
Show that the motion will be governed by the differential equation
$$\ddot{\theta} = -k^2\sin(\theta)\,,$$
where $k$ is a constant to be found.
What sorts of values would $k$ take? Design pendulums which would have $k=0.1, 1$ and $10$.
Whilst this equation might look easy to solve, you will almost certainly not be able to solve it! Why not try, to get a feel for the difficulties involved?
It is common to make the assumption that $\theta$ is small, so that $\sin(\theta)\approx \theta$. Is this a reasonable assumption to make? Test this out by looking at the range of values for which $\sin(\theta)$ is within $1\%$ of $\theta$ (use radians for this, as radians are the natural measure of angle for the trig functions and the units which must be used in series expansions)
What effect does making this approximation have on the solution? By investigating the acceleration on the bob throughout one-quarter cycle of motion (i.e. the first drop to the vertically down position), determine whether the approximation will give a time period which is too large or too small when compared with reality.
Getting Started
You will need to make use of the sort of differential equations encountered in further mathematics to make sense of this problem.
Student Solutions
We were sent a wonderfully detailed solution by Ben from Kenny. He has formatted it beautifully, so we are including his pdf directly. It is well worth reading through.
Furthermore, one of our vacation summer students produced the solution given here.
Equation of motion
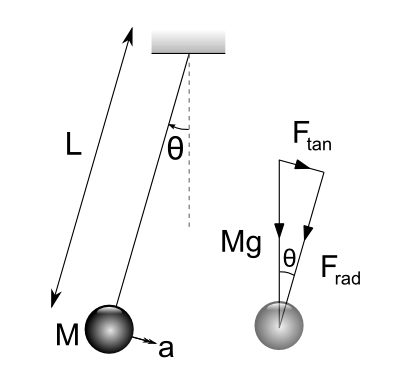
Considering the forces acting on the pendulum bob acting in the tangential direction
$$F_{tan} = Mg \sin \theta$$
Newton's Second Law:
$$\sum_{i}\mathbf{F_i} = \frac{d}{dt}(m \mathbf{v})$$
Applying tangentially:
$$\Rightarrow M a_{tan} = M g \sin \theta \ \Rightarrow \ a_{tan} = g \sin \theta$$
Changing from translational to angular acceleration $a_{tan} = -\ell \ddot{\theta}$ (negative sign due to opposing directions):
$$\Rightarrow-\ell \ddot{\theta} = g \sin \theta$$
$$\therefore \ddot{\theta} = \frac{-g}{\ell} \sin \theta $$
This is a second-order non-linear differential equation in $\theta$. It cannot be solved easily due to the $\sin \theta$ term. An analytical solution is possible, using what are called elliptical integrals, though it is not reducible to elementary functions.
Comparing with $\ddot{\theta} = -k^2 \sin \theta $ gives
$$k^2 = \frac{g}{\ell} \Rightarrow \ell = \frac{g}{k^2}$$
$$k = 0.1 \Rightarrow k^2 = 0.01 \Rightarrow \ell = 100g = 981\textrm{ m}$$
$$k =1 \Rightarrow k^2 = 1 \Rightarrow \ell = g = 9.81\textrm{ m}$$
$$k =10 \Rightarrow k^2 = 100 \Rightarrow \ell = \frac{g}{100} = 0.0981\textrm{ m}$$
Linearisation using small-angle approximation
The Taylor series expansion of the sine function is:
$$\sin \theta = \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \frac{\theta^7}{7!} + O(\theta^9)$$
(where $O(\theta^7)$ indicates terms in $\theta^9$ and above, sometimes called Big-O notation).
For 'small' $\theta$, $O(\theta^3) \ll \theta$ and so $\sin \theta \approx \theta$. 'Small' here has intentionally been left vague as the next part of the question is to consider the validity of this assumption.
To find the range of values for which $\sin \theta$ lies within 1% of $\theta$, find the point at which $\sin \theta$ is exactly $0.99\theta$ (i.e. 1% less).
$\sin \theta = 0.99 \theta$ by numerical methods $\Rightarrow \theta = \pm 0.24532\ \textrm{rad} = \pm 14.1^\circ$
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
Possible support
