The Not-so-simple Pendulum 2
Things are roughened up and friction is now added to the approximate simple pendulum
Problem
A simple pendulum released from rest from an angle $y$ of less that $20^\circ$ is well-modelled by the linear differential equation
$$m\frac{d^2 y}{dt^2} +k^2y=0\;.$$
Can you work out the meaning of the various letters in the equation, the units of the constant $k$, and find the general solution to this equation?
Look at the solution: it keeps on oscillating for ever. Clearly, this is an unreasonable assumption, as real pendulums stop swinging due to friction.
Here friction is modelled by a force term which is directly proportional to the velocity of the object, acting in the opposite direction to the motion. Do you think that this is a good modelling assumption? What are its strengths and weaknesses?
With this assumption, the differential equation becomes
$$m\frac{d^2 y}{dt^2} + \lambda \frac{d y}{dt}+k^2y=0\;.$$
Can you see how this equation satisfies all of requirements of a motion under friction? What are the units of $\lambda$, and what features of the motion would contribute to it in practice? It is assumed that $\lambda$ is constant: is this a reasonable assumption?
Although this equation might look complicated it is still only a second order differential equation with constant coefficients, so can be solved using standard methods (and a lot of algebra) to give
$$y = \exp\Big[-\frac{\lambda t}{2m}\Big]\Big[A\cos(\Lambda t)+\sin(\Lambda t)\Big] \quad\mbox{and}\quad \Lambda = \sqrt{\frac{k^2}{m}-\frac{\epsilon^2}{4m^2}}\;.$$
Test your skills of differentiation by showing that this equation indeed satisfies the differential equation. More importantly, analyse the solution: how well does it model friction? Consider in particular the amplitude and the frequency of the damped oscillation. Does this meet with your intuitive expectation?
Getting Started
Intuitively, how does friction affect motion? Does the $v$ term accomplish this to some level?
How does the equation relate to $F=ma$?
As a rough sketch without any calculation, what would you expect the trajectory over time of the exact, real pendulum motion be over time? Compare this to a plot of the solution. What would be realistic values of the parameters? Make some well-reasoned estimations if you have no intuitive sense for the scale of the parameters.
Student Solutions
We were sent two very impressive solutions to this fascinating problem. We can only assume that Ben from Kenny and Paul (no location given) are going to go on to do great things mathematically!
Both solutions were formatted in careful detail, so we include the two pdf files directly for Paul and Ben. Ben also included his geogebra file for you to have a look at.
Undamped Equation of Motion (with linear approximation)
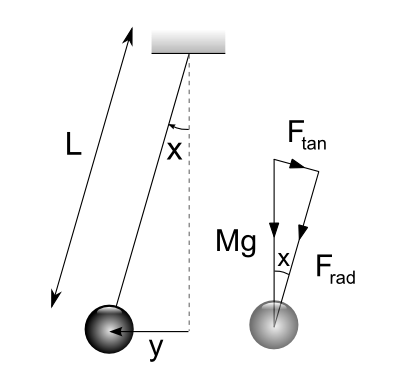
No radial acceleration as $F_{rad}$ balanced by tension in string.
Newton's Second Law:
$$\sum_{i}\mathbf{F_i} = \frac{\textrm{d}}{\textrm{d}t}(m \mathbf{v})\;.$$
Considering the tangential direction:
$$F_{tan} = mg \sin x \quad\textrm{ and }\quad a_{tan} = -\ddot{x} \ell $$
$$\Rightarrow -mg \sin x = m\ddot{x}\ell\;.$$
$\sin x = \frac{y}{\ell}$ from trigonometric definitions $\Rightarrow y = \ell \sin x\;.$
For small $x$ ($x < 20^\circ$ from question), $\sin x \approx x$
$$\Rightarrow y = \ell x \Rightarrow \ddot{x} = \frac{\ddot{y}}{\ell}\;.$$
Substituting:
$$
\begin{align}
mg \frac{y}{\ell} &= -m \frac{\ddot{y}}{\ell} \ell\\
\frac{mg}{\ell}y &= -m\ddot{y}\\
m\ddot{y} + \frac{mg}{l}y &= 0
\end{align}
$$
$\Rightarrow k = \sqrt{\frac{mg}{\ell}}$ with units $\sqrt{\textrm{kg}}\ \textrm{s}^{-1}\;.$
Inclusion of friction (damped response)
$$
\begin{align}
-mg \frac{y}{\ell} - \lambda \frac{\dot{y}}{\ell} \ell &= m \frac{\ddot{y}}{\ell} \ell\\
m\ddot{y} + \lambda \dot{y} + \frac{mg}{\ell} y &= 0\\
m\ddot{y} + \lambda \dot{y} + k^2 y &= 0
\end{align}
$$
$$
\begin{align}
y &= \exp \left[ \frac{-\lambda}{2m} t \right] \left( C \left[ \cos (\Lambda t) + i \sin (\Lambda t) \right] + D \left[ \cos (\Lambda t) - i \sin (\Lambda t) \right] \right)\;,\\
y &= \exp \left[ \frac{-\lambda}{2m} t \right] \left[ (C+D) \cos (\Lambda t) + i(C-D) \sin (\Lambda t) \right]\;.
\end{align}
$$
Let $A = C + D$ and $B = i(C-D)$:
$$y = \exp \left[ \frac{-\lambda}{2m} t \right] \left[ A \cos (\Lambda t) +B \sin (\Lambda t) \right]\;.$$
Therefore,
$$
\begin{align}
\dot{y} &= \frac{-\lambda}{2m} \exp \left[ \frac{-\lambda}{2m} t \right] \left[ A \cos (\Lambda t)+B \sin(\Lambda t) \right] + \exp \left[ \frac{-\lambda}{2m} t \right]\left[ - \Lambda A \sin (\Lambda t) + \Lambda B \cos (\Lambda t) \right]\\
\dot{y} &= \exp \left[ \frac{-\lambda}{2m} t \right] \left[ \left(\Lambda B - \frac{\lambda}{2m}A \right) \cos (\Lambda t) - \left(\Lambda A + \frac{\lambda}{2m}B \right) \sin (\Lambda t) \right]
\end{align}
$$
and
$$
\begin{align}
\ddot{y} &= \frac{-\lambda}{2m} \exp \left[ \left(\Lambda B - \frac{\lambda}{2m}A \right) \cos (\Lambda t) - \left(\Lambda A + \frac{\lambda}{2m}B \right) \sin (\Lambda t) \right] + \\
& \qquad \exp \left[ \frac{-\lambda}{2m} t \right] \left[ -\Lambda \left(\Lambda B - \frac{\lambda}{2m}A \right) \sin (\Lambda t) - \Lambda \left(\Lambda A + \frac{\lambda}{2m}B \right) \cos (\Lambda t) \right]\\
\ddot{y} &= \exp\left[ \frac{-\lambda}{2m} t \right] \left[ \left( \left( \frac{\lambda}{2m} \right)^2 A - 2 \left( \frac{\lambda}{2m} \right) B - \Lambda^2 A \right) \cos (\Lambda t)\right. + \\
& \qquad\left.\left( \left( \frac{\lambda}{2m} \right)^2 B + 2 \left( \frac{\lambda}{2m} \right) A - \Lambda^2 B \right) \sin (\Lambda t) \right]
\end{align}
$$
Substituting back in to $ m\ddot{y} + \lambda \dot{y} + k^2 y = 0$ gives:
$$
\begin{align}
0 =
& m \left\{
\exp \left[ \frac{-\lambda}{2m} t \right] \left[ \left( \left( \frac{\lambda}{2m} \right)^2 A - 2 \left( \frac{\lambda}{2m} \right) B - \Lambda^2 A \right) \cos (\Lambda t) + \right.\right.\\
&\qquad\left.\left.\left( \left( \frac{\lambda}{2m} \right)^2 B + 2 \left( \frac{\lambda}{2m} \right) A - \Lambda^2 B \right) \sin (\Lambda t) \right]
\right\} + \\
& \qquad\lambda \left\{
\exp \left[ \frac{-\lambda}{2m} t \right] \left[ \left(\Lambda B - \frac{\lambda}{2m}A \right) \cos (\Lambda t) - \left(\Lambda A + \frac{\lambda}{2m}B \right) \sin (\Lambda t) \right]
\right\} + \\
& \qquad k^2 \left\{
\exp \left[ \frac{-\lambda}{2m} t \right] \left[ A \cos (\Lambda t) +B \sin (\Lambda t) \right]
\right\}
\end{align}
$$
$$
\begin{align}
0 = \exp \left[ \frac{-\lambda}{2m} t \right]
& \cos (\Lambda t)
\left\{
m \left(\frac{\lambda}{2m}\right)^2 A - 2m \left(\frac{\lambda}{2m}\right) \Lambda B - m \Lambda^2 A + \right.\\
&\qquad\qquad\left.\lambda \Lambda B -\lambda \left(\frac{\lambda}{2m}\right) A + k^2 A
\right\} +
\\
& \sin (\Lambda t)
\left\{
m \left(\frac{\lambda}{2m}\right)^2 B + 2m \left(\frac{\lambda}{2m}\right) \Lambda A - m \Lambda^2 B - \right.\\
&\qquad\qquad\left.\lambda \Lambda A -\lambda \left(\frac{\lambda}{2m}\right) B + k^2 B
\right\}
\end{align}
$$
$$
\begin{align}
0 = \exp \left[ \frac{-\lambda}{2m} t \right]
& \cos (\Lambda t)
\left\{
\left(\frac{\lambda^2}{4m}\right) A - \lambda \Lambda B - m \left( \frac{k^2}{m}-\frac{\lambda^2}{4m^2} \right) A + \right.\\
&\qquad\qquad\left.\lambda \Lambda B -\left(\frac{\lambda^2}{2m}\right) A + k^2 A
\right\} +
\\
& \sin (\Lambda t)
\left\{
\left(\frac{\lambda^2}{4m}\right) B + \lambda \Lambda A - m \left( \frac{k^2}{m}-\frac{\lambda^2}{4m^2} \right) B - \right.\\
&\qquad\qquad\left.\lambda \Lambda A - \left(\frac{\lambda^2}{2m}\right) B + k^2 B
\right\}
\end{align}
$$
$$ \begin{align}
0 = \exp \left[ \frac{-\lambda}{2m} t \right]
& \cos (\Lambda t)
\left\{
\left(\frac{\lambda^2}{4m}\right) A - k^2 A + \left( \frac{\lambda^2}{4m} \right) A -\left(\frac{\lambda^2}{2m}\right) A + k^2 A
\right\} +
\\
& \sin (\Lambda t)
\left\{
\left(\frac{\lambda^2}{4m}\right) B - k^2 B + \left(\frac{\lambda^2}{4m} \right)B - \left(\frac{\lambda^2}{2m}\right) B + k^2 B
\right\}
\end{align}
$$
$$ 0= \exp \left[ \frac{-\lambda}{2m} t \right]
\cos (\Lambda t) \left\{ \left(\frac{\lambda^2}{2m}\right) A - \left(\frac{\lambda^2}{2m}\right) A \right\}
+ \sin (\Lambda t) \left\{ \left(\frac{\lambda^2}{2m}\right) B- \left(\frac{\lambda^2}{2m}\right) B \right\}$$
$$ 0 = \exp \left[ \frac{-\lambda}{2m} t \right] \cos (\Lambda t) \left\{ 0 \right\} + \sin (\Lambda t) \left\{ 0 \right\} = 0$$
$\therefore$ solution is valid.
Taking initial conditions $y(0) = Y_0$ and $\dot{y}(0) = 0$:
$$
\begin{align}
y(0) = Y_0 \Rightarrow & Y_0 = \exp(0) \left[ A \cos (0) +B \sin (0) \right]\\
& Y_0 = (1) \left[ A (1) +B (0) \right] \\
& A = Y_0\\
\end{align}
$$
$$
\begin{align}
\dot{y}(0) = 0 \Rightarrow & 0 = \exp(0) \left[ \left(\Lambda B - \frac{\lambda}{2m} Y_0 \right) \cos (0) - \left(\Lambda Y_0 + \frac{\lambda}{2m}B \right) \sin (0) \right]\\
& 0= (1) \left[ \left(\Lambda B - \frac{\lambda}{2m} Y_0 \right) (1) - \left(\Lambda Y_0 + \frac{\lambda}{2m}B \right) (0) \right] \\
& B = \frac{\lambda Y_0}{2m \Lambda}\\
\end{align}
$$
$$\therefore y = \exp \left[ \frac{-\lambda}{2m} t \right] \left[ Y_0 \cos (\Lambda t) + \frac{\lambda Y_0}{2m \Lambda} \sin (\Lambda t) \right]$$
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
Possible support
