Catalyse That!
Problem
- What rate of heating would give rise to exactly 100 mol being catalysed?
- For heating at a rate of 1 degree per minute, after how long will exactly 100 mol been catalysed?
- (Hard numerical extension) What rate of heating would lead to exactly 100 mol being catalysed in the shortest time?
Notes and background
Whilst the chemistry of certain processes might seem reasonably straightforward, to implement reactions on an industrial scale requires very precise levels of timing, heating and so on. Since a human is unable carefully to watch a reaction progress in many cases, checking mechanisms must be automated. Scaling up reactions to large volumes can introduce many engineering complications not seen in the laboratory.
Furthermore, many chemical and biological reactions will naturally activate once certain temperatures are reached. Measuring a specific quantity of reactants in these cases might be tricky, and the amount taken out of the freezer, for example, might need to be smaller than the amount required for an experiment so as to take into account this (inevitable) continuous growth.
More realistically, heating does not typically occur at a fixed rate. Newton's Law of Cooling tells us that the rate of change in temperature is proportional to the difference in the temperature between the body and the heat source.
Getting Started
Draw a straight line graph to show the rate of reaction.
The amount of chemical produced equals the area under the graph of Rate against Time.
Student Solutions
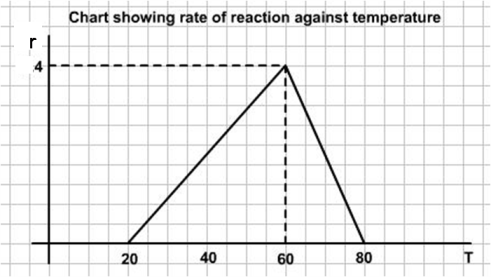
In this problem we are given the graph of rate against temperature. To get the amount catalysed we need to find the graph of rate against time.
Let us call $T$ the temperature, $r$ the rate of reaction and $t$ the time.We are given $R(T)$
So, the rate of reaction $r$ is moles/min/l is given by:
We can easily work out the graph of rate against time for constant heating by noting that after an increase in temperature of $40$ degrees the rate will be $4$ mol/min/l and after a further increase in temperature of $20$ degrees the rate will be back down to zero. For constant rates of heating, the rates will change linearly between these extreme values. For example:
The amount catalysed per litre is the area under the Rate vs Time graph. For these three graphs, the totals are
| Heating Rate (deg / min) | Total Area |
| $2$ | $0.5\times 30\times 4=60$ |
| $1$ | $0.5\times 60\times 4=120$ |
| $0.5$ | $0.5\times 120\times 4=240$ |
To catalyse exactly 100 mol we need to find a rate for which the total area under the rate-time graph is 10 (since we have 10 litres in total). This requires a base of length 5 minutes which corresponds to a rate of heating of $\frac{60}{5} = 12$ degrees per minute (since the temperature needs to increase by 60 degrees in 5 minutes)
Now to find the quickest time to catalyse 100 mol. We could look at the special case $R=1$ asked for in the questions, but can also work it out for a general $R$. The maximal rate of heating is reached after the temperature is raised by 40 degrees, which occurs after a time of $40/R$ minutes. The reaction stops after the temperature is raised by 60 degrees, which occurs after $60/R$ minutes. We have some picture like the following:
Clearly if 100 mol is catalysed before the maximum rate of $4$ is reached, we could decrease the time taken by increasing the rate. So we can assume the the fastest heating assumes a configuration as in the picture (where $X\geq 40/R$).
We need an expression for the maximum time in terms of the rate of heating $R$. To do this we will need to find the area of the shaded quadrilateral.
This just uses simple geometry of lines. The gradient of the second part is $-R/5$. So,
$$
Y = 4 - \left(X-\frac{40}{R}\right)\left(\frac{R}{5}\right)
$$
The area of the shaded quadrilaterial, which is the sum of a triangle and trapezium, must equal 10:
$$
\frac{1}{2}\times\frac{40}{R}\times 4 + \frac{1}{2} \left( 4 + Y \right)\left( X-\frac{40}{R}\right)=10
$$
We want to find the $R$ which minimises $X$, so need to eliminate $Y$ from these equations. We find that
$$
X^2R^2-120 XR+ 100 R+ 2400 = 0
$$
Wc can look numerically at solving the quadratic for various values of $R$. We find this curve:
The optimal heating rate is about 10.8 degrees per minute.
Note: A tricky exercise in calculus shows that the exact optimal rate of heating is
$$24\left(-2+\sqrt{6}\right)$$
There is an alternative way to approaching this problem, which does not rely on graphs, but purely on calculus. Below is the solution using this approach, as well as a solution for the final part of the question and also the extension.
1) Let the rate of reaction be denoted $r$, the rate of heating $R$, the temperature $T$ and $t$ as time.
Using the data given in the question, it is possible to write for 10 litres of solution:
$ r = T - 20\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 20 \leq T \leq 60$
$r = 40 - 2(T-60) = 160 - 2T\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 60 \leq T \leq 80$
Also, as $R$ is the rate of change of temperature:
$\frac{dT}{dt} = R$
$\rightarrow T = Rt + c$
Since $t = 0$, $T = 20$
$\therefore c =20$
$\rightarrow T = Rt + 20$
This final equation can be put back into the initial equations for rate, so that the rate is now dependent on time rather than on temperature. The limits are also changed to be dependent on time too:
$ r = Rt \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 \leq t \leq \frac{40}{R}$
$ r = 120 -2Rt \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{40}{R} \leq t \leq \frac{60}{R}$
Rate, $r$, is the rate of change of product with time. Therefore:
$r = \frac{dP}{dt}$
$P = \int r dt$
Integrating the two equations for rate across their respective ranges, and then summing them together gives:
$P = [\frac{Rt^2}{2}]_0^{\frac{40}{R}} + [120t - Rt^2]_{\frac{40}{R}}^{\frac{60}{R}} = \frac{1200}{R} = 100$
$\mathbf{\therefore R = 12^{\circ}\ C\ min^{-1}}$
2) $R = 1^{\circ}\mbox{C min}^{-1}$
Since $R = \frac{dT}{dt} = 1$
$\therefore T = t + 20$ as before.
$ r = T - 20\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 20 \leq T \leq 60$
$r = 40 - 2(T-60) = 160 - 2T\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 60 \leq T \leq 80$
Putting these two expressions together to eliminate T gives:
$ r = t \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 \leq t\leq 40$
$ r = 120 -2t \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 40 \leq t \leq 60$
$\therefore P = 100 = \int^t_0 r\ dt = \int^t_0 t\ dt = [\frac{t^2}{2}]^t _0$
$\rightarrow \mathbf{t = 10\sqrt{2} \approx 14.14\ mins}$
3) As in (1) we have :
$ r = Rt \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 \leq t \leq \frac{40}{R}$
$ r = 120 -2Rt \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{40}{R} \leq t \leq \frac{60}{R}$
We reason that the fastest time for making 100 moles must be > $\frac{40}{R}$, otherwise the rate of heating could be increased indefinitely to decrease the time necessary.
Thus $ P = 100 = \int r\ dt = [\frac{Rt^2}{2}]^{\frac{40}{R}}_0 + [120t - Rt^2]^t_{\frac{40}{R}}$
$\therefore R^2t^2 -120Rt + 100R + 2400 =0$
We are trying to find the value of $R$ which minimises $t$. First, it is necessary to get an expression for $t$ by using the quadratic formula, which simplifies to:
$t = \frac {60 \pm \sqrt{1200 -100R}}{R}$
To find the minimum value of $t$, requires differentiating with respect to $R$ and making this equal to zero:
$\frac{dt}{dR} = \mp \frac{50}{R\sqrt{1200-100R}} + \frac{1}{R^2}(-60 \mp \sqrt{1200 - 100R}) = 0$
It can now be seen that one of these equations can be rejected. The equation in which all the terms are negative must be rejected because it cannot equal zero unless R is infinite. This leaves the other equation, which can be rearranged to:
$120 - 5R =6\sqrt{1200-100R}$
Squaring this equation and then solving the formed quadrative gives:
$R = 24( -2 \pm \sqrt{6})$
Clearly the negative root needs to be rejected, leaving:
$R = \mathbf{24 (\sqrt{6} -2)}$ in order to give the minimum time to make 100 moles.
4) The problem now is one of cooling. The mixture is initially at 100$^{\circ}$C and allowed to cool. As before, the same rate is observed at a particular temperature, although adjusted for 1 litre as opposed to 10 litres:
$ r = \frac{T - 20}{10}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 20 \leq T \leq 60$
$r = \frac{40 - 2(T-60)}{10} = \frac{160 - 2T}{10}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 60 \leq T \leq 80$
$r = 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ T \geq 80$
The rate of change of temperature is now $-R$ as opposed to $R$, and $T = 100$ at $t = 0$:
$\frac{dT}{dt} = -R$
$T = -Rt + 100 $
Combining these equations to eliminate $T$ yields:
$ r = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ t\leq \frac{20}{R}$
$r = \frac{2Rt -40}{10} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{20}{R} \leq t \leq \frac{40}{R}$
$r = \frac{80 -Rt}{10} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{40}{R}\leq t \leq \frac{80}{R}$
Again, to find the value of $R$ required to create exactly 100 moles of product, we must integrate these rates across the appropriate ranges and set them equal to 100. This yields:
$\mathbf{R = \frac{140}{3} \approx 46.7^{\circ}C\ min^{-1}}$
Extension:
Let $T_o$ be the temperature of the oven.
$R = \frac{dT}{dt}\ \alpha \ T_o - T$
$\therefore \frac{dT}{dt} = k(T_o - T)$ where k is an unknown constant of proportionality.
$\int_0^T \frac{dT}{T_o -T} = \int_0^t k\ dt$
$[-ln(T_o -T)]^T_0 = kt$
Rearraging this expression to make $T$ the subject gives:
$T = T_o(1 - e^{-kt})$
As before, this expression can be used with the rate expressions to eliminate $T$ and so provide a rate equation in terms of $t$. Additionally, it is possible to change the limits of these. Thus, integration of these rate equations are possible, in order to give yields of product in terms of time. With the appropriate value of $k$ and $T_o$ these will give actual values.
Teachers' Resources
Why do this problem?
This task is an exercise in understanding rates of change, graphs and (possibly) calculus in a way which does not use the usual route of speed-time graphs.Possible approach
Key questions
The key questions should be used to help learners to understand that the amount catalysed equals the area under the graph of Rate against Time. For the straight line graphs involved here, simple calculation of areas will be enough. Learners should be given plenty of thinking or discussion time before being prompted with these key questions:- What does the graph of rate of reaction against temperature look like?
- Will the reaction always lead to at least 100 mol being catalysed?
- Why would a very fast rate of heating give rise to a very small amount of chemical being catalysed?
- If the oven heated the compound to exactly 21 degrees, how long would it take to catalyse 100 moles?
- If the oven heated the compound at 1 degree per minute, how much would be catalysed in total?
- If the oven heated the compound at 2 degrees per minute, how much would be catalysed in total?
