Can't find a coin?
Can you generate a set of random results? Can you fool the random
simulator?
Problem
Imagine your teacher has set you the homework task of throwing a coin 100 times and carefully recording your results in the order that they appear. Imagine that you can't be bothered to go and find a coin - the task is just too tedious. So you decide to try to fool your teacher.
How will you go about it?
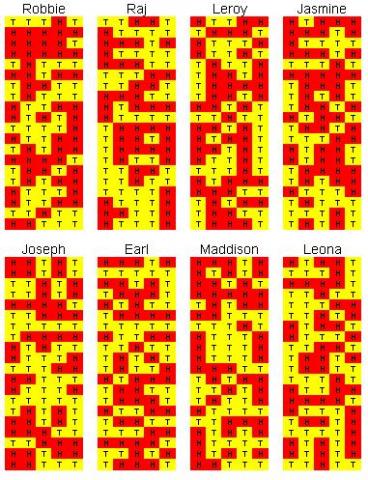
One of these students made up their homework results, which one is the most suspicious?
BACKGROUND INFORMATION
Whilst all combinations of Heads and Tails are equally likely, certain sets of results (such as all heads or alternating Heads and Tails all the way) would look rather suspicious. Why is this?
The computer here is programmed to determine whether the set of Heads and Tails falls into a suspicious category or not. Rather interestingly, if you do generate the Heads and Tails truly randomly using a coin then there is a 95% chance the the computer will know that these were generated randomly. Don't believe it? Try it out!
How will you go about it?
One of these students made up their homework results, which one is the most suspicious?
Image
BACKGROUND INFORMATION
Whilst all combinations of Heads and Tails are equally likely, certain sets of results (such as all heads or alternating Heads and Tails all the way) would look rather suspicious. Why is this?
The computer here is programmed to determine whether the set of Heads and Tails falls into a suspicious category or not. Rather interestingly, if you do generate the Heads and Tails truly randomly using a coin then there is a 95% chance the the computer will know that these were generated randomly. Don't believe it? Try it out!
Getting Started
How often do you expect the result from a throw to be the same as the result from the previous throw?
How often do you expect to get a run of three identical results?
How often do you expect to get a run of four identical results?
How often do you expect to get a run of five identical results?...
Student Solutions
Nabeelah from Langley Grammar School commented that:
Your teacher won't know whether you have cheated or not
because they can't know what happend because the result can be
anything.
Of course this is right but your results
could be suspicious if they are very unlikely to occur.
Some people suggested ways in which to get results that appeared likely.
Eloi fromSt. Patrick's Catholic Primary School went about it like this:
Some people suggested ways in which to get results that appeared likely.
Eloi fromSt. Patrick's Catholic Primary School went about it like this:
We used a coin for the first twenty then we did something
similar to it to get our solution.
Phil used this strategy that managed to fool
the computer:
I started by making them all heads. I then flipped every
second coin. Then I flipped every third coin, then every 5th, 7th,
11th, 13th, 17th ... until I'd gone through all the prime numbers.
The computer was sure these were random.
Thomas from High Storrs suggested this:
The best way of making the results seem random is not having equal numbers of heads and tails. If you decide to have more heads then have large groups of heads with a few tails in between in groups of three. If you alter the size of the groups of heads then the results appear random.
Philippa from Ashcroft Academy worked
out that Earl had the most suspicious results:
I think Earl is the cheat because his heads and tails are pretty
much equal as if he tried too hard to simulate the random pattern
of a coin.
Another way of telling that Earl is the most likely cheat is to notice that he has no strings of repeated results of length of 5 or more, and when you realise that there are 95 strings of 6 consecutive results (1st, 2nd, 3rd, 4th, 5th and 6th - 2nd, 3rd, 4th, 5th, 6th and 7th - 3rd, 4th, 5th, 6th, 7th and 8th...) you may find it suspicious that long strings of repeated results do not appear at all.
