Road maker 2
Problem
This problem follows on from Road Maker, where the rules of making roads are detailed in full.
The Munchkin road making authority have commissioned you to work out the possible destinations for their roads. Use Cartesian coordinates where the first tile is placed with opposite corners on $(0,0)$ and $(1,1)$.
Investigate ways in which you can reach your destination. You may like to consider these questions:
- Can you make roads with rational values for the $x$ coordinate of the destination?
- Can you make roads with rational values for the $y$ coordinate of the destination?
- Can you create a road with the $x$ coordinate equal to any integer multiple of one half?
- Can you make roads for which the coordinates of the destination are both rational? Both irrational?
- Can multiple roads lead to the same destination? For which destinations is the road unique?
Getting Started
You might like to consider working out the destinations of these paths. It is helpful to move along each path one tile at a time and record the coordinates of one of the vertices as you go.
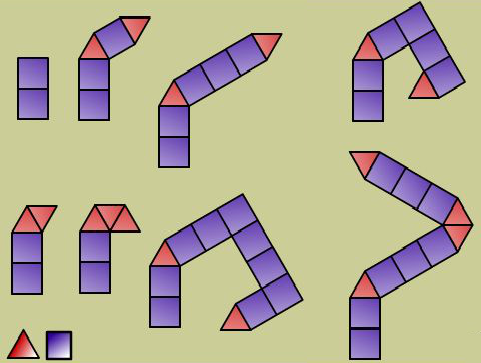
Student Solutions
This is quite interesting. The key idea is based on this picture:
Once you get the hang of it you can easily count your way around any path. Paths can be arranged so that the irrational part cancels out by having equal numbers going up/down or equal numbers going left/right.
Dapeng Wang from Claremont School sent in a good solution to this problem. His idea was to analyse different possible combinations of two shapes. We present his basic idea but formulate it slightly differently below.
Suppose we have constructed a Munchkin road. The first tile is required to have a corner at the point $(0,0)$. It is clear when we think about it that the destination of the road (i.e. the top/bottom vertex of the last triangle) can be reached by tracing a path from $(0,0)$ along edges of the shapes that make up the road. We set up an induction argument. $(0,0)$ is obviously of the form
$(\frac{a+b\sqrt{3}}{2},\frac{c+d\sqrt{3}}{2})$. Now suppose we choose a path from $(0,0)$ to the destination of the road. Pick a vertex on this path, which has coordinates $(x,y)$ say. All edges in the road have length $1$.Bearing in mind that the triangles are equilateral, it is clear that the angle to the horizontal of any edge must be a multiple of $30^{\circ}$. Therefore the next vertex in
the path must be one of $(x\pm 1,y)$, $(x,y\pm 1)$, $(x\pm\frac{1}{2},y\pm\frac{\sqrt{3}}{2})$ or $(x\pm\frac{\sqrt{3}}{2},y\pm\frac{1}{2})$. By induction, then, any vertex on the path, and in particular the destination of the path, is of the form$(\frac{a+b\sqrt{3}}{2},\frac{c+d\sqrt{3}}{2})$.
Teachers' Resources
Why do this problem?
Provide training in conjecture, mathematical analysis and proof. This difficult problem requires students to realise that it is possible to use counting (a discrete process) to somehow categorise different paths. This gives the power to make general statements.
Possible Approach?
First students need to calculate the end points of a few simple roads. Although there are rational and irrational endpoints, group discussion should lead to the conclusion that root 3 should be involved in the irrational endpoints in some way.
Key Questions?
If you have a valid road, how can its endpoint change with the addition of a single tile? Two tiles?
