A first product Sudoku
Given the products of adjacent cells, can you complete this Sudoku?
Problem
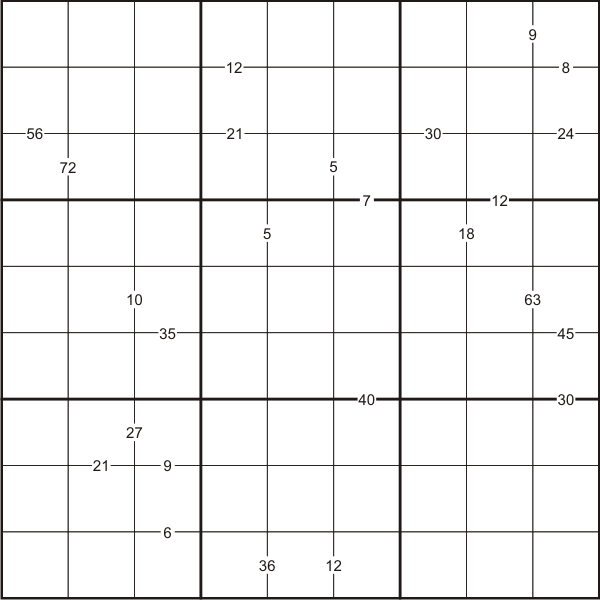
Like the standard Sudoku, this Sudoku consists of a grid of nine rows and nine columns subdivided into nine 3x3 subgrids.
Like the standard Sudoku, it has two basic rules:
1. Each column, each row and each box (3x3 subgrid) must have the numbers 1 to 9
2. No column, row or box can have two squares with the same number.
The puzzle can be solved with the help of clue-numbers which are small numbers written on the intersections between two cells. Each clue-number is the product of the two digits in the two cells that are on either side of it.
For example, 8 in the top right box means that possible pairs of numbers for the cells above and below are either 1 and 8, 8 and 1, 4 and 2, or 2 and 4 respectively.
You may find it useful to print out a copy of the First Product Sudoku.
Getting Started
Rosie and Zoe solved this Sudoku, their journey can be found here. The order with which they filled the Sudoku is marked in the boxes. This is one possible method of many to help you solve the problem.
Student Solutions
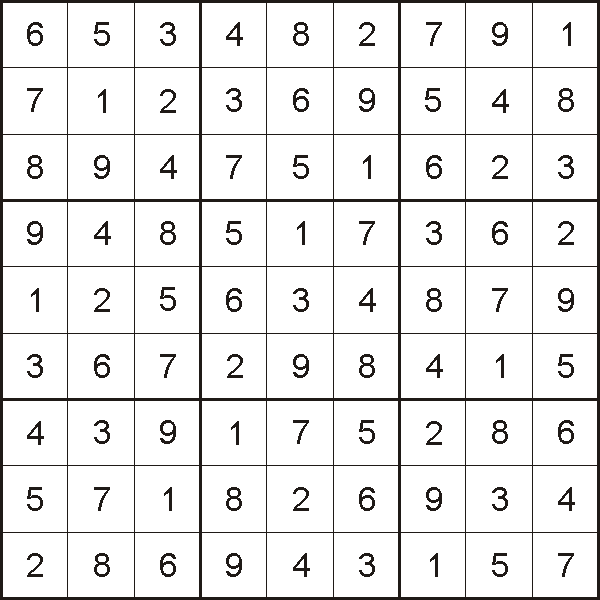
Answer:
First, use the numbers where there is only one factor pair of numbers 1-9. Use numbers where the factors need to overlap.
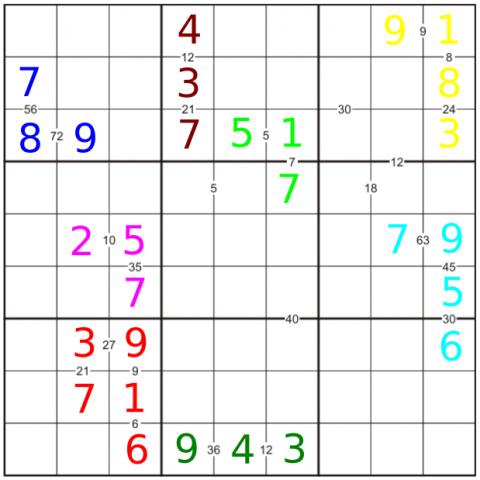
Now we can use the ones we've got to decide which way round the other factors should go. Remember that each number should appear only once in each row, column and 3x3 box.

Continue, using the rules of sudoku.

