Overlapping Again

Stage: 2 Challenge Level:

Overlapping Again

You may want to look at Overlaps before you try this problem.

Here are some pairs of shapes:

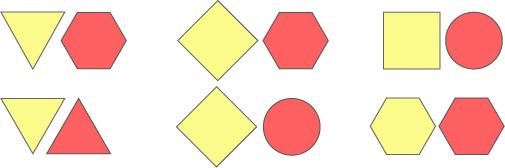
What overlap shape would you get if you overlapped them halfway across each other?

Here are some more pairs of shapes. What overlap shapes would you get this time?

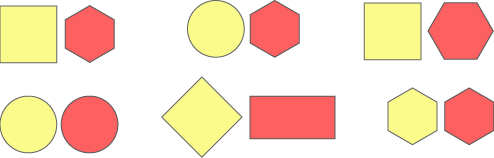
Which of these overlap shapes did you find?

You may like to use this interactivity to experiment after you have tried to imagine what will happen in your head.

Full screen version

This text is usually replaced by the Flash movie.

Why do this problem?

This problem, as in Overlaps, focuses on encouraging children to visualise - in this case to picture an image in their head. There are also valuable opportunities for them to apply their knowledge of properties of shape and to use appropriate vocabulary.

Visualising can be a very useful way of getting into a problem, as well as helping at other stages of the problem-solving process. Providing opportunities like this for your class to practise visualising will help them become familiar with its uses and to regard it as a legitimate skill to draw upon.

Key questions

What are the two shapes you are thinking about?

Looking at the overlaps where the sides are diagonal, which shapes could they have come from?

Can you imagine gradually moving one shape across the other one?

Possible extension

Learners who need more of a challenge could try Quadrilaterals.

Possible support

Suggest trying this simpler version of the problem.

Quadrilaterals. Practical Activity. Games. Pentagons. Compound transformations. Circles. Interactivities. Hexagons. Visualising. Equilateral triangles.