Prime Magic

Place the numbers 1, 2, 3,..., 9 one on each square of a 3 by 3 grid so that all the rows and columns add up to a prime number. How many different solutions can you find?

Fifteen

Can you spot the similarities between this game and other games you know? The aim is to choose 3 numbers that total 15.

Flip Flop - Matching Cards

A game for 1 person to play on screen. Practise your number bonds whilst improving your memory

Difference Sudoku

Stage: 3 and 4 Challenge Level:

By Henry Kwok

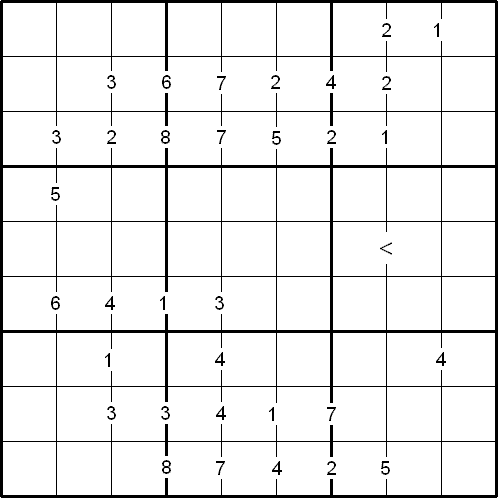
Rules of Difference Sudoku

Like the standard sudoku, the object of the puzzle is to fill in the whole $9 \times 9$ grid with numbers $1$ through $9$ so that each row, each column, and each of the nine $3 \times 3$ squares must contain all the nine different numbers.

There are special clue-numbers placed on the border lines between selected pairs of adjacent squares of the grid. Each clue-number is the difference between the two numbers that should be in the adjacent squares just next to left & right from that clue-number.

For example, a clue-number $7$ on the border line between two adjacent squares means that possible pairs of numbers for these squares must be from the following combinations: $1$ and $8$; $2$ and $9$; $8$ and $1$; or $9$ and $2$.

The inequality sign, which is placed on the border line between r5c7 (row 5 column 7) and r5c8, indicates that the number in r5c7 is smaller than the number in r5c8. As this variant has only one inequality sign on the border line, it is called Minimal Difference Sudoku.

A word document containing the problem can be found here, for use in the classroom.