Shape Times Shape
These eleven shapes each stand for a different number. Can you use the number sentences to work out what they are?
Problem
Shape Times Shape printable sheet
The coloured shapes stand for eleven of the numbers from 0 to 12. Each shape is a different number.
Can you work out what they are from the multiplications below?
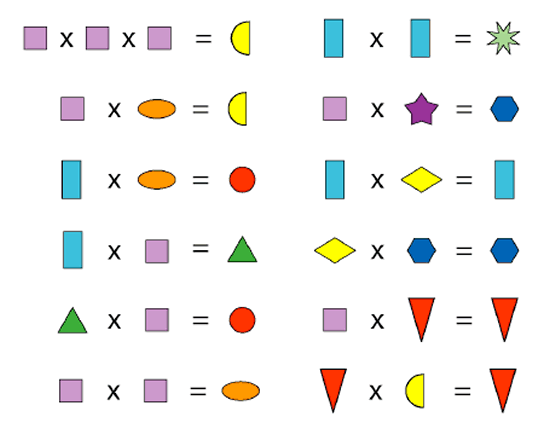
For accessibility, clicking on the 'show' button below will show a description of this image.
Square × square × square = semicircle
Square × oval = semicircle
Oblong × oval = circle
Oblong × square = equilateral triangle
Equilateral triangle × square = circle
Square × square = oval
Oblong × oblong = eight-pointed star
Square × five-pointed star = hexagon
Oblong × rhombus = oblong
Rhombus × hexagon = hexagon
Square × isosceles triangle = isosceles triangle
Isosceles triangle × semicircle = isosceles triangle
Click here for a poster of this problem.
You may be interested in the other problems in our Number Fluency Feature.
Getting Started
Where could you start?
What can you tell from the first multiplication with three purple squares and a yellow semi-circle?
Perhaps you can use what you now know to help you with another calculation?
How will you remember what you have tried and what you have found out? You could use this sheet to keep a note of what you think the shapes stand for.
Student Solutions
We had correct solutions from Nayel of St. James C of E; Alexus of the Australian International School Malaysia; children from Saint Stephen's College Australia; Isaac, Emily and Chloe from Edward Bryant; Matthew from New Hill Primary; Freya and Ava, Patrick, Logan and Aiden from Crofton Hammond; Caitlin from Walthamstow Hall; Joey from The Harrow School Bangkok; Chelsea and Presley from St Josephs School in Australia; Jake from Boulcott School in New Zealand; Lidia and Honey, and Joe, from Hazlehead Primary; Almina and Luca, Lewis and Amera, Kane and Olivia, and Emily and Jude from St Monans Primary.
Ginny from Westridge School for Girls sent in the following:
I started with the first sentence, which is the square times square times square equals semi-circle one. I used the process of elimination to figure it out. Because, it couldn't have been 1, since then multiple shapes would have the same number. And it couldn't have been 3, because that would've made the semi-circle's value larger than 12. So, I settled on 2.
After filling out the spots where the squares and semi-circles were used, I started creating a key which would state the values I had found.
Next, I looked at the second sentence, which was easy since there was only one spot available, so the answer was obvious.
After that, I repeated the action of filling out the rest of the shapes with the value I found. I continued doing this, sometimes using the process of elimination until I had only one shape left. This shape was the upside down triangle, or cone. I was confused, since 1 was already taken, and only 7 was left. After pondering it some, I remembered I could use the 0, and the problem was solved.
Mr Robinson's group at Powers Hall Academy described what happened:
We have explored this problem and worked systematically. We found that square could not be 1 or 3 as square would re-occur or be too big, so it would have to be 2.
We already knew that square was 2, so square squared is 4. Therefore oval is 4.
4 x 2 = 8 so semicircle is 8.
We estimated that rectangle would be between 4 and 2 so it was 3.
When we explored further, we found that triangle is 6 and circle is 12.
In both sentences with inverse (upside down) triangle, the answer was inverse triangle so inverse triangle is 0.
In both sentences with rhombus, the answer was the shape that wasn't the rhombus so rhombus is 1.
Rectangle is 3 and 3 x 3 is 9.
We predicted star = 5 so 2 x 5 = 10 and hexagon is 10.
Inverse triangle = 0; Rhombus = 1; Purple Square = 2; Rectangle = 3; Oval = 4; Star = 5; Triangle = 6; Semi circle = 8; Double star = 9; Hexagon = 10; Circle = 12.
We found that 11 and 7 couldn't be in there as 11 x 2 = 22 and 22 is too great. 7 x 2 = 14 and 14 is too great. They are both prime so can't be included.
Szymon, Charlie and Hattie from Edward Bryant School sent in a good explanation:
We realised that anything times the isosceles triangle equaled the isosceles triangle, so it must be 0.
Then we figured out that the only cubed number below 12 was 2 because 1 would make it be another square as the answer, when it was a half-circle. That made the half-circle have a value of 8.
We knew that something times 2 equaled 8 so we then realised that the oval must be 4.
Next, we did the rectangle times rectangle and worked out that it was 3 because the only number squared that we could use was 3, as we had already used 2.
After that, we did the rectangle times square which made the equilateral triangle equal 6.
Then, we did the equilateral triangle times the square which made the circle 12.
We then realised that the eight-pointed star must be 9 because 3 times 3 made 9.
We saw that the rectangle times diamond equaled rectangle, so the diamond was 1.
We then worked out the hexagon because the square times anything would be an even number and the only one we had left was 10.
That made the five-pointed star equal 5.
The two numbers that had nothing to represent were 7 and 11.
Rhea from Sutton School sent in a very well presented, thought-out solution:
Firstly, we know what the purple square is because it is x cubed and because the shapes each stand for a number between 0 and 12 there is only one possibility, 2. It cannot be 1, because 1 cubed is 1 and the answer to the calculation is a different shape. It cannot be 3 because 3 cubed is 27 seven and 27 is greater than 12.
By working out what number the square represents we can work out that the semi-circle is 8 (2 cubed - 2 x 2 x 2).
We can work out the oval because the sum shows the square - which we know is two times the oval equals the semi circle - which we know is 8. Then we do 8 divided by 2 which equals 4 to find out the value of the oval.
Next we can work out the circle. There are two calculations which can help us do this. The rectangle times the oval (4) = circle and the triangle times the square (2) = the circle. We know that the value of the circle must be a factor of 4 and 2 and the only three numbers are 4, 8 and 12. 4 is the value of the oval and 8 is the value of the semi-circle so the red circle must be 12.
From this, we can work out that the rectangle is 3 (12 - circle divided by 4 - oval) and the green triangle is 6 (12 - circle divided by 2 - square). We can work out what the eight-pointed star is because there is a calculation showing the rectangle (3) times the rectangle (3) which equals 9. Next we can work out the diamond. The rectangle (3) times the diamond equals the rectangle (3). To find out the diamond we do 3 divided by 3 which equals 1. We can check this with diamond (1) time hexagon = hexagon. This makes sense because one multiplied by any number (not zero) will be the number you multiplied by one. We can also work out the red triangle.
The square (2) multiplied by the red triangle equals the red triangle and the red triangle multiplied by the semi-circle (8) = the red triangle. The only possible value of the red triangle is zero, because anything multiplied by zero equals zero.
Now we only need to find out two more shapes, the purple star and the hexagon. The only sum which will help us is the square (2) multiplied by the purple star equals the hexagon. There isn't a way to work it out mathematically so we must see what we already know to work out what the value of the two shapes are. So far, we know...
Square=2; Semi-circle=8; Oval=4; Rectangle=3; Circle=12; Green Triangle=6; 8 Pointed Star=9; Diamond=1; Red Triangle=0.
The only three numbers from 0-12 which aren't in the list are 5, 7 and 10. The sum is square (2) multiplied by the purple star equals the hexagon. The only numbers which make sense in the sentence are 5 and 10. Therefore, the purple star must equal 5 and the hexagon must equal 10.
An excellent explanation! Well done.
Cecilia, Diya, Egor, Jack, Julia, Leo, Louise, Sweder, Tea and Vincent from The International School, Brussels sent their very clear work, that you can view here.docx .
Thank you all for you hard work in trying to explain your thinking.
Teachers' Resources
Why do this problem?
Possible approach
As you circulate, listen out for clear reasoning, based on learners' knowledge of number properties. You may wish to warn some pairs that you will be asking them to share their thinking with everyone later. It would be worth stopping everyone for a brief mini plenary before that if you notice some interesting and efficient ways to record.
Tamara Pearson, a teacher from Atlanta, US, wrote to us to say she had adapted this task and created her own version using Adinkra symbols. Thank you, Tamara.
Key questions
What does that tell us? How do we know?
