Rectangle rearrangement
A 3x8 rectangle is cut into two pieces... then rearranged to form a right-angled triangle. What is the perimeter of the triangle formed?
Age
14 to 16
Challenge level
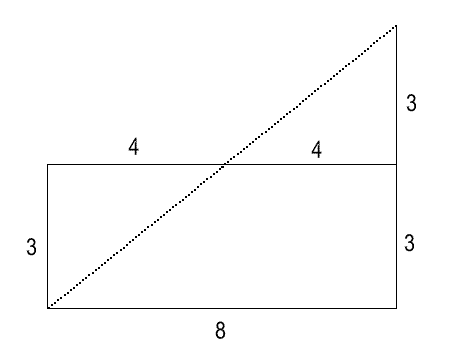
Problem
A $3 \times8$ rectangle is cut into two pieces along the dotted line shown. The two pieces are then rearranged to form a right-angled triangle. What is the perimeter of the triangle formed?
Image
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
The diagram shows the two pieces will fit together to form a right-angled triangle which has a base $8$ and height $6$. The length of the hypotenuse = $\sqrt{(6^2+8^2)}$, that is $10$, so the perimeter of the triangle is $24$.
Image
