Trapezium Arch
Weekly Problem 27 - 2007
Ten stones form an arch. What is the size of the smallest angles of the trapezoidal stones?
Ten stones form an arch. What is the size of the smallest angles of the trapezoidal stones?
Problem
Image

If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Sachdave from Doha College in Qatar used exterior angles, marked $\text a$ in the diagram below. Sachdave's method was similar to this:
Image
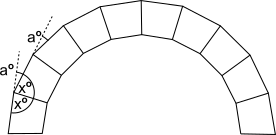
Tracing around the arch, it is necessary to turn through $\text{a}^\text{o}$ nine times, or ten times to end up facing in the opposite direction from where you started. You would also turn through $180^\text{o}.$
So $\text a = 180\div10 = 18$. Then notice that $\text{a, } x$ and ${x}$ make a straight line, so $\text a + 2x = 180,$ so $2 x = 162,$ so $x = 81.$
Sameer from Hymers College and Kira and Emma from Wycombe High School in the UK considered the angles in a regular icosagon (twenty-sided polygon). Sameer said:
Image

In any regular polygon, the sum of the exterior angles is $360^\text{o}.$ As there are $20$ exterior angles, each one is $360^\text{o}\div20$, which is $18^\text{o}.$
The interior angle is $180^\text o-$ exterior angle, which will be $180^\text o-18^\text o=162^\text o.$ This is shown in the diagram.
The interior angle forms a circle with the smaller angles of the trapeziums. In a circle, all the angles add up to $360^\text o.$
The two angles marked $y^\text o$ intersecting this circle are the same, so $$\begin{align}360&=162+2y\\ \Rightarrow 198&=2y\\ \Rightarrow y&=99\end{align}$$
In a trapezium, the angles add up to $360^\text o,$ so $$\begin{align}2x+2y&=360\\ \Rightarrow x+y&=180\\ \Rightarrow
x+99&=180\\ \Rightarrow x&=81\end{align}$$
Sophie from the Stephen Perse Foundation used triangles:
Image

$$180^\text{o}\div10=18^\text o$$
Image

$\dfrac{180-18}{2}=81$ which is shown on the diagram.
Angles on a straight line add up to $180^\text o$
$180-81=99$ which is shown on the diagram.
Considering the trapezium below the triangle,
$$\begin{align}99\times2&=198\\\frac{360-198}{2}&=81\end{align}$$
Image

Thank you also to Toby from Chairo Christian School in Australia, who submitted a correct solution.
