Curvature of Surfaces

Stage: 5

Article by Alan and Toni Beardon

How curved is a curve? How curved is a surface? When is a 'curved surface' flat? We shall only briefly mention curves in the plane and then move on to discuss positive and negative curvature of surfaces.

Imagine tracing out the ellipse shown in the diagram. How does the curvature change as you go around the ellipse? Without applying any mathematics everyone would agree that the tightest bends are at the ends and the least curvature on the track around the ellipse is halfway between these points .

To measure the curvature at a point you have to find the circle of best fit at that point. This is called the osculating (kissing) circle. The curvature of the curve at that point is defined to be the reciprocal of the radius of the osculating circle. We shall not discuss in this article the method for finding this radius accurately which needs calculus. Suffice it to say that this circle has not only the same tangent at the point (the first derivatives being the same) but also the curve and the osculating circle have the same second derivatives at the point.

Why use the reciprocal in defining curvature? It is natural for the curvature of a straight line to be zero. Imagine straightening out a curve making it into a straight line. In the limit the circle of best fit has infinite radius giving zero curvature.

The diagram shows osculating circles to the ellipse at points A, B and C. At A the curvature is ${2\over 3}$, at B it is ${1\over 12}\approx 0.083$ and at C it is $0.288$.

The following equations are given in case you want to plot the graphs yourself, but ignore them if not and read on.

The equation of this ellipse is $${x^2\over 36} + {y^2\over 9}=1.$$ At the point on the ellipse $(x,y) = (a\cos \theta, b\sin\theta)$ with $(a=6,\ b=3)$, the curvature is given by $${ab\over (a^2\sin^2 \theta+ b^2\cos^2 \theta)^{3/2}}.$$

A perfect sphere has constant curvature everywhere on the surface whereas the curvature on other surfaces is variable. For example on a rubgy ball the curvature is greatest at the ends and least in the middle. Measuring curvature at a point using curves through that point on the surface will not work. Which plane curve should we use? At the '2' on the rugby ball, the curve in one direction, going between the B and the E, has greater curvature than the curve along the length of the ball.

Gauss proved that, taking the curvatures in all directions at a point on a surface, the product of the maximum and minimum curvatures at the point is constant when the surface is distorted provided that lengths in the surface are unchanged.

One method used to measure the Gaussian curvature of a surface at a point is to take a small circle of radius $r$ on the surface with centre at that point and to calculate the circumference or area of the circle. If the circumference is $2\pi r$ and the area is $\pi r^2$ the surface is flat and is said to have zero curvature. If the circumference is less than $2\pi r$ and the area is less than $\pi r^2$ the surface has positive curvature; if the circumference is greater than $2\pi r$ and the area is greater than $\pi r^2$ the surface has negative curvature. There are three distinct geometries for the three types of surfaces and each of these geometries has its own trigonometry with the results in each trigonometry having counterparts in the other two trigonometries. Euclidean geometry is the geometry of surfaces with zero curvature. Spherical geometry, also known as elliptic geometry, is the geometry of surfaces with positive curvature. Hyperbolic geometry is the geometry of surfaces with negative curvature. See the article How Many Geometries Are There? .

can baked beans

What about the curvature of the surface of a cylinder? Clearly the top and bottom are flat but what about the surface, often called the curved surface, where the label is wrapped around as in the illustration? Along the length of the cylinder the curvature is zero and in other directions there is positive curvature so the product of the maximum and minimum curvatures is zero making the Gaussian curvature zero. To see this another way, unwrap the label and you can flatten it out, draw a small circle of radius $r$ anywhere on the label and it has a circumference of $2\pi r$ and an area of $\pi r^2.$ Wrap the label around the can again and the circumference and area of the circle you have drawn do not change as the paper takes the shape of the surface of the cylinder. So the surface of the cylinder has zero Gaussian curvature.

In order to find the areas of circles on spheres we shall use a result discovered by Archimedes of Syracuse who invented calculus type methods almost two thousand years before Newton and Leibniz. Archimedes made many discoveries and inventions including the Archimedean Screw pump, still in use today, depicted on this stamp, and you can find out more about him on the St Andrew's website. The result we shall use is depicted in the diagram on the right and said to have been on Archimede's tombstone.

The cylinder shown has radius $r$, height $2r$ and area $4\pi r^2$, the same as the surface area of the sphere inside. Moreover the area of a strip on the surface of a sphere cut off by two parallel planes is equal to the area cut off by the planes on the circumscribing cylinder.

In this cross section, A and B are planes at a small distance dy apart, cutting the sphere and circumscribing cylinder. The 'triangle' with sides dy, dx and dc is so small that we can treat the arc dc as if it were a straight line and the hypotenuse of this triangle. This tiny triangle is similar to the triangle shown with sides $x, y$ and $r$ so that $${dy\over dc} = {x\over r}.$$

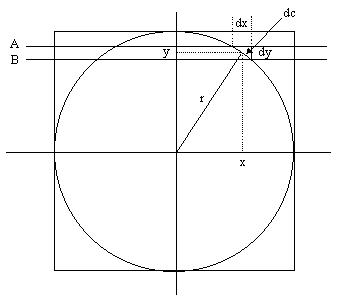
The area of the strip cut off by planes A and B on the surface of the sphere is $2\pi xdc$ because this strip has circumference $2\pi x$ and height dc.\par The area of the band on the cylinder is $2\pi rdy$. As we have shown that $xdc=rdy$ it follows that these areas are equal.

Now we study the curvature of the surface of a sphere of unit radius. Take any point N and draw a circle centre N radius $r$ on the surface of the sphere where the radius is an arc in the surface of the sphere subtending an angle of $r$ radians at the centre of the sphere.

The circumference of the circle centre N radius $r$ is $2\pi \sin r$. Because $\sin r < r$ for all non-zero values of $r$ we see that this circumference $2\pi \sin r$ is less that $2\pi r$ showing that the surface has positive curvature..

By Archimedes' method the area of this circle is $2\pi r(1 -\cos r).$ You can verify that this is less than $\pi r^2$, and hence that the curvature of the surface of the sphere is positive, by drawing the graphs of $y=\cos x$ and $y = 1 - {x^2\over 2}$ on the same axes and showing that $\cos r > 1 - {r^2\over 2}.$

It is harder to model surfaces of negative curvature like a saddle between two hills, the surfaces of cooling towers, banana skins etc.A banana has positive curvature on the outside of the 'bend' of the banana and negative curvature on the inside.

Imagine you are at the lowest point on the saddle between the two hills shown in the picture below.

Tie a long rope to a post at this point and, keeping the rope taught, walk around a circle with the post as centre. As you have to walk uphill and downhill as well as around the post you walk farther than you would walk on flat ground showing that the curvature at that point is negative.

Gaussian curvature is closely linked to the angle deficiency of the surface at that point. If the surface is flat and you draw a circle centred at that point you go around 360 degrees.

At the red spot on the cube the angle deficiency is $90^o$, the circumference of a circle of radius $r$ with centre at the red spot on the cube is ${3\over 4}\times 2\pi r$ so the curvature at that point is positive. The curvature is concentrated at the vertices of the cube rather than being distributed over the surface as with a sphere or a rugby ball shaped solid. Although the curvature is concentrated at 16 points, the block shown with a hole through it is analagous to the torus (or doughnut shaped solid) shown in yellow.

We investigate the curvature at the red spot at the edge of the hole in the block. The angle deficiency at the red spot is $-90^o$. The circumference of a circle of radius $r$ with centre at the red spot on the block is ${5\over 4}\times 2\pi r$ so the curvature at that point is negative.

You can check for yourself the property (equivalent to Euler's formula) that the total angle deficiency for any polyhedron is 720 degrees. The total angle deficiency for a solid depends on the number of holes in the solid. For solids with one hole the total angle deficiency is zero.

To read more on the subject of Gaussian curvature without getting deep into higher mathematics see this article and related articles from a workshp on 'Geometry and The Imagination' led by John Conway, Peter Doyle, Jane Gilman and Bill Thurston.

2D representations of 3D shapes. Curvature. physics. Geodesics. Maths Supporting SET. Length/distance. Spheres. Arcs, sectors and segments. Non Euclidean Geometry. Torus.