Round and round and round
Problem
Round and Round and Round printable worksheet
This problem follows on from Going Round in Circles.
Watch the film below.
Imagine the dot starts at the point $(1,0)$, turns through $60$ degrees anticlockwise and then stops.
I was wondering, if the point hadn't stopped, and instead carried on until it had turned through $30$ $000$ degrees, might it have finished the same distance above the horizontal axis?
I took out my calculator and typed $30$ $000$ $\div$ $360$
The answer on the screen was $83.333333$.
How can I use this to help me solve my problem?
There are ideas for follow-up problems in the Notes .
Getting Started
What does $0.333333$... mean?
What fraction is equivalent to $0.1111111$...?
If the dot turns through $10$ degrees anticlockwise it will be the same distance above the horizontal axis as if it had turned through $170$ degrees anticlockwise. Can you see why?
Student Solutions
Jacob (Tunbridge Wells Grammar School for Boys) worked out that it had turned 120 degrees:
"83.3 recurring and this represents the number of turns. 83.3 recurring turns is the same as 83 1/3 turns. Each full turn returns the dot to the starting point, and so the point finished 120 degrees anti-clockwise from its starting position."
Nikolaus then spotted that the point at 120 degrees has been rotated 30 degrees anticlockwise from the blue vertical line, whereas the point at 60 degrees has been rotated 30 degrees clockwise, and so this is the same height:
"When it goes 60 degrees anticlockwise it is 30 degrees (clockwise) from the 90 degrees line and 1/3 of a turn is 120 degrees which is 30 degrees (anticlockwise) from the blue 90 degree line, and as the circle is symmetrical this is the same vertical height from the horizontal axis."
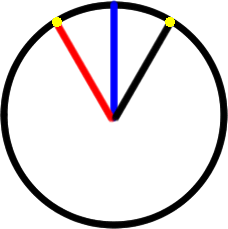
Alternatively, for those of you who may have met trigonometry, Rafael spotted that the distance from the dot to the horizontal axis is actually the sine function, and so knew that sin60=sin120, so the heights were the same.
Teachers' Resources
This problem offers students an opportunity to test their understanding of division and to consider different ways in which calculators can be used.
The interactivity also offers students a chance to explore the relationships between the angles of turn that produce the same vertical and horizontal displacements.
This printable worksheet may be useful: Round and Round and Round
Follow up questions could include:
Imagine the dot starts at the point $(1,0)$, turns through $20$ $000$ degrees anticlockwise and then stops.
Through what angle(s) between $0$ and $360$ degrees would the dot have had to turn if it was to finish the same distance above/below the horizontal axis?
If I type $20$ $000$ $\div$ $360$ into my calculator the answer on the screen is $55.555556$
How can this help me answer the question?
Similarly for $40$ $000$ degrees.
If I type $40$ $000$ $\div$ $360$ into my calculator the answer on the screen is $111.11111$.
Similarly for $80$ $000$ degrees.
If I type $80$ $000$ $\div$ $360$ into my calculator the answer on the screen is $222.22222$.
Similarly for $250$ $000$ degrees.
If I type $250$ $000$ $\div$ $360$ into my calculator the answer on the screen is $694.44444$.
And what about horizontal displacements to the left/right of the vertical axis?
Students could make up their own questions...