Triangle numbers
Problem
Triangle Numbers printable worksheet
In the multiplication square below, the first eleven triangle numbers $1$, $3$, $6$, $10$, $15$, $21$, $28$, $36$, $45$, $55$, $66$ have been identified.
Can you see a pattern?
Can you predict the positions of the next triangle numbers?
Check to see if you're right.
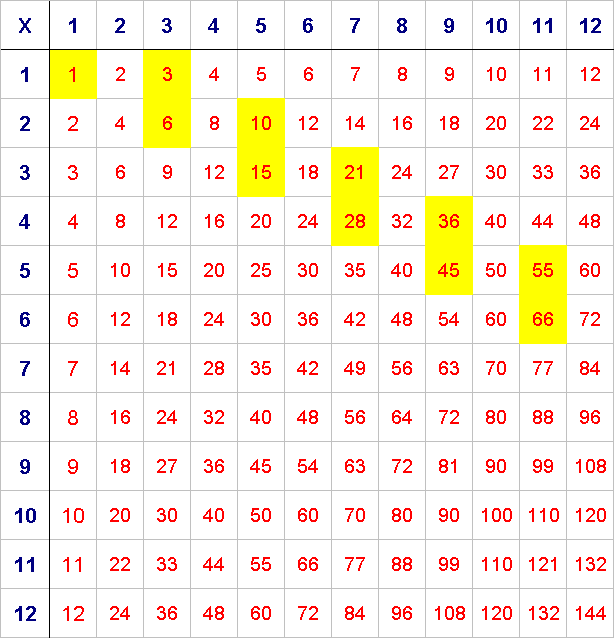
Can you explain why triangle numbers take up these positions in a multiplication square?
Thank you to Paul Stephenson from The Magic Mathworks Travelling Circus who provided the idea for this problem.
Getting Started
The first triangle number is $1$
The second triangle number is $1 + 2$
The third triangle number is $1 + 2 + 3$
The fourth triangle number is $1 + 2 + 3 + 4 \ldots$
The $n^{\text{th}}$ triangle number is $\frac{n(n+1)}{2}$
Student Solutions
Well done Amelia and Kahlia from Ardingly College, Lauren from St. Matthew's School and Kate from Orston Primary for realising that the pattern would continue indefinitely.
Kahlia reminded us that
"Triangle numbers are numbers which can form a triangle."$1$
$1 + 2$
$1 + 2 + 3$
$1 + 2 + 3 + 4 $
$1 + 2 + 3 + 4 + 5 $
$1 + 2 + 3 + 4 + 5 + 6 $
$1 + 2 + 3 + 4 + 5 + 6 + 7$
we add an even number, then an odd number, then another even number, then another odd number, and so on.
Lauren noticed that:
"All the odd numbers along the top e.g. $1, 3, 5, 7, 9, 11$ have a couple of triangle numbers underneath."And Kate noticed that:
"The difference between the two triangular numbers above and below each other on the table square is the same as the number at the top.e.g. the difference between $3$ and $6$ is three, which is above them on the square."
So that clarifies why we go down from one triangle number to another along odd numbered columns when the difference between the triangle numbers is odd.
On each row we move two squares across, so that takes care of having to add the next even number:Moving two squares across on the first row adds $2$
Moving two squares across on the second row adds $4$
Moving two squares across on the third row adds $6$
And so on.
So, moving across adds the next even number, moving down adds the next odd number:
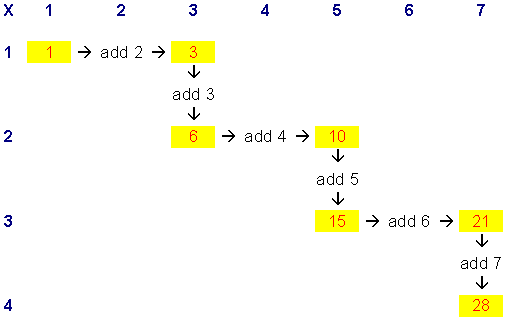
Paul offered another way to think about it:
Teachers' Resources
Why do this problem?
This problem allows students to investigate the relationship between triangle numbers expressed as a sum and triangle numbers expressed visually. Students may focus on either representation to arrive at a conclusion. The problem can be concrete with students focusing on small numbers or can be extended to give a general result.
Possible approach
This printable worksheet may be useful: Triangle Numbers .
You could discuss the structure of triangle numbers as a sum (i.e. add $2$, then $3$, then $4$, then $5$, etc.) and then ask students to describe the visual layout of the triangle numbers coloured in the grid. Students can then experiment on paper to try to spot patterns from which a general conjecture might be made.
Key questions
- What can you see in the grid?
- Where would you expect the next pair of triangle numbers to go? Were you correct?
- Can you describe how to move from one triangle number to the next?
- What does moving one square down the multiplication grid do to the number?
- What is the effect of moving across by one column in the grid?
Possible support
Providing grids for students to draw on might make the connections clearer.
Possible extension
- Can you create a general algebraic expression for the $n$th triangle number?